题目内容
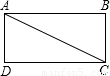
(2011•普陀区二模)如图,矩形纸片ABCD的边长AB=4,AD=2.翻折矩形纸片,使点A与点C重合,折痕分别交AB、CD于点E、F,(1)在图中,用尺规作折痕EF所在的直线(保留作图痕迹,不写作法),并求线段EF的长;
(2)求∠EFC的正弦值.
【答案】分析:(1)作AC的垂直平分线即为EF,易得AC的值,利用∠1在不同直角三角形中的正切值可得EO的长,乘以2即为EF的值;
(2)作EH⊥CD于H,∠EFC的正弦值=BC:EF,代入计算即可.
解答: 解:(1)作图正确(2分)
解:(1)作图正确(2分)
∵矩形ABCD,
∴∠B=90°,BC=AD.
∵在Rt△ABC中,AB=4,AD=2
∴由勾股定理得:AC=2 .(1分)
.(1分)
设EF与AC相交于点O,
由翻折可得AO=CO= ,∠AOE=90°.
,∠AOE=90°.
∵在Rt△ABC中,tan∠1= ,
,
在Rt△AOE中,tan∠1= .
.
∴ ,(1分)
,(1分)
∴EO= .(1分)
.(1分)
同理:FO= .
.
∴EF= .(1分)
.(1分)
(2)过点E作EH⊥CD垂足为点H,(1分)EH=BC=2(1分)
∴sin∠EFC= .(1分)
.(1分)
点评:本题主要考查了解直角三角形的知识;利用∠1在不同直角三角形中相同的正切值求解是解决本题的突破点.
(2)作EH⊥CD于H,∠EFC的正弦值=BC:EF,代入计算即可.
解答:
 解:(1)作图正确(2分)
解:(1)作图正确(2分)∵矩形ABCD,
∴∠B=90°,BC=AD.
∵在Rt△ABC中,AB=4,AD=2
∴由勾股定理得:AC=2
 .(1分)
.(1分)设EF与AC相交于点O,
由翻折可得AO=CO=
 ,∠AOE=90°.
,∠AOE=90°.∵在Rt△ABC中,tan∠1=
 ,
,在Rt△AOE中,tan∠1=
 .
.∴
 ,(1分)
,(1分)∴EO=
 .(1分)
.(1分)同理:FO=
 .
.∴EF=
 .(1分)
.(1分)(2)过点E作EH⊥CD垂足为点H,(1分)EH=BC=2(1分)
∴sin∠EFC=
 .(1分)
.(1分)点评:本题主要考查了解直角三角形的知识;利用∠1在不同直角三角形中相同的正切值求解是解决本题的突破点.

练习册系列答案
相关题目
 的⊙C与x轴交于A(-1,0)、B(3,0)两点,且点C在x轴的上方.
的⊙C与x轴交于A(-1,0)、B(3,0)两点,且点C在x轴的上方.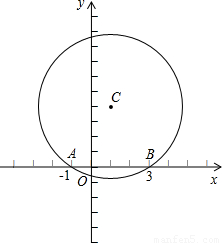
 .
.