题目内容
某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=-
| 1 |
| 100 |
若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
| 1 |
| 100 |
(1)当x=1000时,y=
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
分析:(1)将x=1000代入函数关系式求得y,并根据等量关系“利润=销售额-成本-广告费”求得w内;
(2)根据等量关系“利润=销售额-成本-广告费”“利润=销售额-成本-附加费”列出两个函数关系式;
(3)对w内函数的函数关系式求得最大值,再求出w外的最大值并令二者相等求得a值;
(4)通过对国内和国外的利润比较,又由于a值不确定,故要讨论a的取值范围.
(2)根据等量关系“利润=销售额-成本-广告费”“利润=销售额-成本-附加费”列出两个函数关系式;
(3)对w内函数的函数关系式求得最大值,再求出w外的最大值并令二者相等求得a值;
(4)通过对国内和国外的利润比较,又由于a值不确定,故要讨论a的取值范围.
解答:解:(1)x=1000,y=-
×1000+150=140,
w内=(140-20)×1000-62500=57500.
(2)w内=x(y-20)-62500=-
x2+130x-62500,
w外=-
x2+(150-a)x.
(3)当x=-
=6500时,w内最大;
由题意在国外销售月利润的最大值与在国内销售月利润的最大值相同,得:
=
,
解得a1=30,a2=270(不合题意,舍去).
∴a=30.
(4)当x=5000时,w内=337500,w外=-5000a+500000.
若w内<w外,则a<32.5;
若w内=w外,则a=32.5;
若w内>w外,则a>32.5.
∴当10≤a<32.5时,选择在国外销售;
当a=32.5时,在国外和国内销售都一样;
当32.5<a≤40时,选择在国内销售.
| 1 |
| 100 |
w内=(140-20)×1000-62500=57500.
(2)w内=x(y-20)-62500=-
| 1 |
| 100 |
w外=-
| 1 |
| 100 |
(3)当x=-
| 130 | ||
2×(-
|
由题意在国外销售月利润的最大值与在国内销售月利润的最大值相同,得:
| 0-(150-a)2 | ||
4×(-
|
4×(-
| ||
4×(-
|
解得a1=30,a2=270(不合题意,舍去).
∴a=30.
(4)当x=5000时,w内=337500,w外=-5000a+500000.
若w内<w外,则a<32.5;
若w内=w外,则a=32.5;
若w内>w外,则a>32.5.
∴当10≤a<32.5时,选择在国外销售;
当a=32.5时,在国外和国内销售都一样;
当32.5<a≤40时,选择在国内销售.
点评:本题是一道综合类题目,考查了同学们运用函数分析问题、解决问题的能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为W内(元)(利润 = 销售额-成本-广告费).
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为W内(元)(利润 = 销售额-成本-广告费).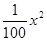 元的附加费,设月利润为W外(元)(利润 = 销售额-成本-附加费).
元的附加费,设月利润为W外(元)(利润 = 销售额-成本-附加费). x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润 = 销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润 = 销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费).
x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费). 的顶点坐标是
的顶点坐标是 .
. x+150,
x+150, x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费).
x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费). 的顶点坐标是
的顶点坐标是 .
.