题目内容
ab＜0，a＞0，|a|＞|b|，则a+b
- A.大于0
- B.小于0
- C.小于或等于0
- D.无法确定
A
分析：首先根据ab＜0，可判断a、b为异号，再根据a＞0，可得b＜0，因为|a|＞|b|，也就是正数的绝对值大，根据有理数的加法法则：绝对值不等的异号两数相加，取绝对值较大的加数符号，可得a+b＞0．
解答：∵ab＜0，
∴a、b为异号，
∵a＞0，
∴b＜0，
∵|a|＞|b|，
∴a+b＞0，
故选：A．
点评：此题主要考查了有理数的乘法，与有理数的加法，关键是熟练掌握有理数的加法与乘法法则．
分析：首先根据ab＜0，可判断a、b为异号，再根据a＞0，可得b＜0，因为|a|＞|b|，也就是正数的绝对值大，根据有理数的加法法则：绝对值不等的异号两数相加，取绝对值较大的加数符号，可得a+b＞0．
解答：∵ab＜0，
∴a、b为异号，
∵a＞0，
∴b＜0，
∵|a|＞|b|，
∴a+b＞0，
故选：A．
点评：此题主要考查了有理数的乘法，与有理数的加法，关键是熟练掌握有理数的加法与乘法法则．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
6、已知：如图，梯形ABCD是等腰梯形，AB∥CD，AD=BC，AC⊥BC，BE⊥AB交AC的延长线于E，EF⊥AD交AD的延长线于F，下列结论：①BD∥EF；②∠AEF=2∠BAC；③AD=DF；④AC=CE+EF．其中正确的结论有（ ）
如图，在平面直角坐标系中，四边形OABC是矩形，OA=4，AB=2，直线
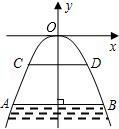如图所示，有一座抛物线形拱桥，桥下面在正常水位AB时，宽20m，水位上升3m就达到警戒线CD，这时水面宽度为10m．
如图，∠ABC=∠DCB=90°，AB=BC，点E是BC的中点，EA⊥ED．