题目内容
若分式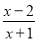 的值为0,则x的值为( )
的值为0,则x的值为( )
A. 2或-1 B. 0 C. 2 D. -1
C 【解析】【解析】 由题意得: ,解得:x=2.故选C.
练习册系列答案
相关题目
下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 若用电量为8千瓦时,则应交电费4.4元
D. y是x的反比例函数
D 【解析】解:A.x与y都是变量,且x是自变量,y是因变量,是函数,正确; B.用电量每增加1千瓦时,电费增加0.55元,正确; C.若用电量为8千瓦时,则应交电费为0.55×8=4.4元,正确; D.y是x的正比例函数,故错误; 故选D.


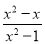 的值为零的所有x的值是( )
的值为零的所有x的值是( )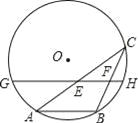

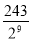 B.
B. 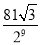 C.
C. 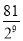 D.
D.