题目内容
已知⊙O是Rt△ABC的外接圆，∠C=90°，AC=3，
与
的度数之比为3：1，则BC的长是（ ）
 |
| AB |
|
| BC |
A、3
| ||
B、2
| ||
C、
| ||
| D、不能确定 |
考点：圆周角定理,圆心角、弧、弦的关系
专题：
分析：根据圆周角定理证明AB是直径，则
是180°，即可求得
的度数，进而求得∠A的度数，利用三角函数求解．
|
| AB |
|
| BC |
解答：解：∵∠C=90°，
∴AB是圆的直径，
∴
是180°，则
的度数是：
×180°=60°，
∴∠A=30°，
∴BC=AC•tan30°=3×
=
．
故选C．
∴AB是圆的直径，
∴
|
| AB |
|
| BC |
| 1 |
| 3 |
∴∠A=30°，
∴BC=AC•tan30°=3×
| ||
| 3 |
| 3 |
故选C．
点评：本题考查了圆周角定理，正确根据定理求得∠A的度数是关键．
练习册系列答案
相关题目
，计算当n=3，5，7，9时的结果，看看会有什么规律．
如图，圆柱的底面半径为2cm，当圆柱的高由小到大变化时，圆柱的体积也发生了变化．下列函数中，是二次函数的是（ ）
| A、S=2t-3 | ||
| B、S=22+5t | ||
| C、y=x2 | ||
D、y=x2-20+
|
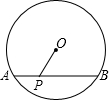如图，⊙O的直径为10，弦AB的长为8，P为弦AB上不同于A，B的一点．若OP的长为整数，则满足条件的点P有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
如图，从小区的某栋楼的A，B，C，D四个位置向对面楼方向看，所看到的范围的大小顺序是（ ）| A、A＞B＞C＞D |
| B、D＞C＞B＞A |
| C、C＞D＞B＞A |
| D、B＞A＞D＞C |
如图，一枚半径为r的硬币沿着直线滚动一圈，圆心经过的距离是（ ）| A、4πr | B、2πr |
| C、πr | D、2r |
