题目内容
【题目】如图,正方形ABCD的边长为3cm,点P从点A出发沿AB→BC→CD以3cm/s的速度向终点D匀速运动,同时,点Q从点A出发沿AD以1cm/s的速度向终点D匀速运动,设P点运动的时间为ts,△APQ的面积为Scm2,下列选项中能表示S与t之间函数关系的是( )
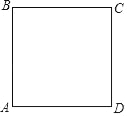
A. 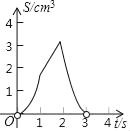 B.
B. 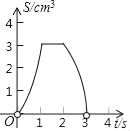
C. 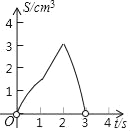 D.
D. 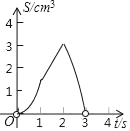
【答案】D
【解析】分析:分①0<t≤1;②1<t≤2;③2<t<3三种情况分别求出S与t之间的函数关系式,再根据二次函数的图象与性质求解即可.
详解:由题意可知,A、P、Q三点构成三角形时,0<t<3,Q在边AD上.
分三种情况:
①0<t≤1时,P在边AB上.
∵AP=3t,AQ=t,
∴S=![]() APAQ=
APAQ=![]() ×3tt=
×3tt=![]() t2,所以B、C错误;
t2,所以B、C错误;
②1<t≤2,P在边BC上.
∵AQ=t,
∴S=![]() AQAB=
AQAB=![]() t3=
t3=![]() t;
t;
③2<t<3,P在边CD上.
∵DP=9-3t,AQ=t,
∴S=![]() AQDP=
AQDP=![]() t(9-3t)=-
t(9-3t)=-![]() t2+
t2+![]() t=-
t=-![]() (t-
(t-![]() )2+
)2+![]() ,所以A错误;
,所以A错误;
故选D.

练习册系列答案
相关题目