Question

【题目】如图，在平面直角坐标系中，点，点分别在轴和轴的正半轴上，且满足.

(1)求点、点的坐标；

(2)若点从点出发，以每秒1个单位长度的速度沿射线CB运动，连结AP，设的面积为，点的运动时间为秒，求与的函数关系式，并写出自变量的取值范围；

(3)在(2)的条件下，是否存在点,使得以点、、为顶点的三角形与相似，若存在，请求出点的坐标；若不存在，请说明理由.

Answer 1

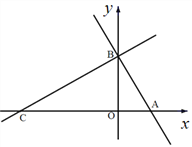
【答案】（1）A的坐标为（1，0），B的坐标为；

（2）当0≤t＜时， ，当t＞时， ；

（3）P的坐标是（-3,0）或（3,2）或（1， ）或（1， ）

【解析】试题分析：（1）根据非负数的性质得到OA、OB的长，即可得到点A、B的坐标；

（2）根据勾股定理得到CB的长度，再根据三角形面积公式即可得到点A到直线CB的距离；再根据△ABP的面积=△ABC的面积-△ACP的面积，即可求出S与t的函数关系式．

（3）先求得∠ABC=90°，然后分两种情况讨论即可求得．

试题解析：（1）∵

∴OB2–3=0且OA–1=0

∴, OA=1

∵点分别在轴和轴的正半轴上

∴A的坐标为（1,0），B的坐标为

(2)∵C的坐标是（-3,0）

∴OC=3，又∵OA=1，OB=

∴BC=2 ，AB=2, AC=4

∴BC2+AB2=AC2 ∴∠ABC=90°

①当0≤t＜时，BP=-t,

②当t＞时，

∴S=

(3)∵∠ABP=∠AOB=90°

∴ΔABP与ΔAOB相似分两种情况讨论：

①当ΔABP∽ΔAOB时， 即, 得

∴P的坐标是（-3,0）或（3,2）

②当ΔABP∽ΔBOA时， 即, 得

过P作PH⊥AC于H,则OB∥PH,易求PH=, OH=1或PH=,OH=1

即P的坐标是（-1， ）或（1， ）

综上所述：P的坐标是（-3,0）或（3,2）或（1， ）或（1， ）