题目内容
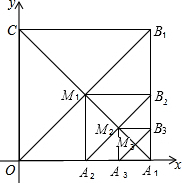 (2011•宜州市一模)如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1,以M1A1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标为( )
(2011•宜州市一模)如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1,以M1A1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标为( )分析:根据正方形的性质得到OM1=M1A1,∠OM1A1=90°,设OM1=M1A1=x,由勾股定理得到方程x2+x2=12,解方程求出x的值,同理可以求出其它正方形的边长,进而得到M1的坐标,M2的坐标,…,依此类推可求出第n个正方形对角线交点Mn的坐标.
解答:解:设正方形的边长为1,
则正方形四个顶点坐标为O(0,0),C(0,1),B1(1,1),A1(1,0),
在正方形OA1B1C中,
∴OM1=M1A1,∠OM1A1=90°,
设OM1=M1A1=x,
由勾股定理得:x2+x2=12,
解得:x=
,
同理可求出OA2=A2M1=
,A2M2=
,A2A3=
,…,
根据正方形对角线定理得M1的坐标为( 1-
,
);
同理得M2的坐标为( 1-
,
);
M3的坐标为( 1-
,
),
…,
依此类推:Mn坐标为( 1-
,
)=(
,
).
故选A
则正方形四个顶点坐标为O(0,0),C(0,1),B1(1,1),A1(1,0),
在正方形OA1B1C中,
∴OM1=M1A1,∠OM1A1=90°,
设OM1=M1A1=x,
由勾股定理得:x2+x2=12,
解得:x=
| ||
| 2 |
同理可求出OA2=A2M1=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
根据正方形对角线定理得M1的坐标为( 1-
| 1 |
| 2 |
| 1 |
| 2 |
同理得M2的坐标为( 1-
| 1 |
| 22 |
| 1 |
| 22 |
M3的坐标为( 1-
| 1 |
| 23 |
| 1 |
| 23 |
…,
依此类推:Mn坐标为( 1-
| 1 |
| 2n |
| 1 |
| 2n |
| 2n-1 |
| 2n |
| 1 |
| 2n |
故选A
点评:本题主要考查对正方形的性质,坐标与图形性质,解一元二次方程,勾股定理等知识点的理解和掌握,能根据求出的数据得到规律是解此题的关键.

练习册系列答案
相关题目
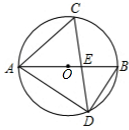 (2011•宜州市一模)如图,AB是⊙O的直径,弦DC与AB相交于点E,若∠ACD=60°∠ADC=50°,∠CAD=70°,则∠ABD的度数为( )
(2011•宜州市一模)如图,AB是⊙O的直径,弦DC与AB相交于点E,若∠ACD=60°∠ADC=50°,∠CAD=70°,则∠ABD的度数为( )