题目内容
(1)x(x-2)=x-2
(2)x2+4x-1=0
解:(1)原式可化为:x(x-2)-(x-2)=0,即(x-2)(x-1)=0,
解得x1=2,x2=1;
(2)原方程可化为:x2+4x+4-4-1=0,即(x+2)2=5,
解得x+2=± ,x1=-2+
,x1=-2+ ,x2=-2-
,x2=-2- .
.
分析:(1)先把移项,再把方程化为两个因式积的形式,求出x的值即可;
(2)先把方程化为完全平方的形式,再用直接开方法求解.
点评:本题考查的是一元二次方程的因式分解法及配方法,需熟练掌握.
解得x1=2,x2=1;
(2)原方程可化为:x2+4x+4-4-1=0,即(x+2)2=5,
解得x+2=±
 ,x1=-2+
,x1=-2+ ,x2=-2-
,x2=-2- .
.分析:(1)先把移项,再把方程化为两个因式积的形式,求出x的值即可;
(2)先把方程化为完全平方的形式,再用直接开方法求解.
点评:本题考查的是一元二次方程的因式分解法及配方法,需熟练掌握.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
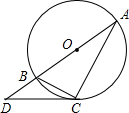 已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A. ,求AD的长.
,求AD的长. 的解集是
的解集是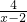 有意义.
有意义. 如图a∥b,若∠1=120°,则∠2的度数是________°.
如图a∥b,若∠1=120°,则∠2的度数是________°.