题目内容
【题目】点C为直线AB上一点,点M、N分别是线段AC、线段BC的中点。
(1)如图,若C为线段AB上一点,AC=6,BC=4,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示);
的代数式表示);
(3)若C为线段AB的延长线上一点,且满足AC-BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示)。
的代数式表示)。
![]()
【答案】(1)5;(2)![]() a;(3)
a;(3)![]() b.
b.
【解析】
(1),根据线段中点的定义得到MC=![]() AC=3、NC=
AC=3、NC=![]() BC=2,然后利用线段的和差关系MN=MC+NC进行计算;
BC=2,然后利用线段的和差关系MN=MC+NC进行计算;
(2),根据线段中点的定义得到MC=![]() AC,NC=
AC,NC=![]() BC,同理利用MN=MC+NC即可得到MN的长;
BC,同理利用MN=MC+NC即可得到MN的长;
(3),首先可根据题意画出图形,然后同理利用线段中点的定义得到MC=![]() AC、NC=
AC、NC=![]() BC,进而依据MN=MC-NC求解即可.
BC,进而依据MN=MC-NC求解即可.
(1)因为点M、N分别是AC、BC的中点,
所以MC=![]() AC=
AC=![]() ×6=3,NC=
×6=3,NC=![]() BC=
BC=![]() ×4=2,
×4=2,
所以MN=MC+NC=3+2=5;
(2)因为点M、N分别是AC、BC的中点,
所以MC=![]() AC,NC=
AC,NC=![]() BC,
BC,
所以MN=MC+NC=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() a;
a;
(3)如图所示.
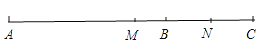
因为点M、N分别是AC、BC的中点,
所以MC=![]() AC,NC=
AC,NC=![]() BC,
BC,
所以MN=MC-NC=![]() AC-
AC-![]() BC=
BC=![]() (AC-BC)=
(AC-BC)=![]() b.
b.
故答案为:(1)5;(2)![]() a;(3)
a;(3)![]() b.
b.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目