题目内容
如图，已知⊙O中，半径OA⊥OB，则∠ACB是
- A.45°
- B.90°
- C.60°
- D.30°
A
分析：由半径OA⊥OB，得∠AOB=90°，根据圆周角定理，即可求出∠ACB．
解答：∵OA⊥OB，
∴∠AOB=90°，
∴∠ACB=90°÷2=45°．
故选A．
点评：本题考查了圆周角定理．同弧所对的圆周角相等，并且等于它所对的圆心角的一半．
分析：由半径OA⊥OB，得∠AOB=90°，根据圆周角定理，即可求出∠ACB．
解答：∵OA⊥OB，
∴∠AOB=90°，
∴∠ACB=90°÷2=45°．
故选A．
点评：本题考查了圆周角定理．同弧所对的圆周角相等，并且等于它所对的圆心角的一半．
练习册系列答案
口算能手系列答案
相关题目
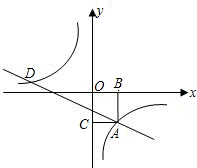过A点的双曲线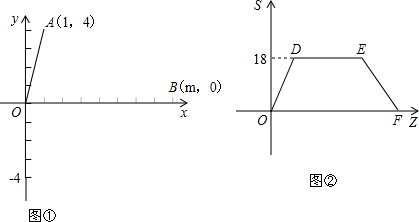
角形均相似（全等可作相似的特殊情况）？如果存在，求出点Q的坐标；如果不存在，请说明理由．
（2012•中山一模）如图，已知等腰梯形ABCD的边BC在x轴上，点A（0，3）在y轴的正半轴上，点D的坐标为（2，3），且AB=
上，CD交AB于F，且∠BDC=∠BAC．