题目内容
 (2011•镇海区模拟)如图,半径为3的动圆⊙P,其圆心点P可在二支双曲线y=
(2011•镇海区模拟)如图,半径为3的动圆⊙P,其圆心点P可在二支双曲线y=| 6 | x |
(2,3)或(3,2)或(-2,-3)或(-3,-2)
(2,3)或(3,2)或(-2,-3)或(-3,-2)
.分析:根据圆在双曲线的两支上,与x标轴、y轴相切,分情况进行讨论计算.
解答:解:①当⊙P在第一象限,与x轴相切时,y=3,
∴
=3,
解得x=2,
与y轴相切时,x=3,
∴y=
=2,
∴点P的坐标是(2,3)或(3,2);
②当⊙P在第三象限,与x轴相切时,y=-3,
∴
=-3,
解得x=-2,
与y轴相切时,x=-3,
∴y=
=-2,
∴点P的坐标是(-2,-3)或(-3,-2).
综上所述,点P的坐标是(2,3)或(3,2)或(-2,-3)或(-3,-2).
故答案为:(2,3)或(3,2)或(-2,-3)或(-3,-2).
∴
| 6 |
| x |
解得x=2,
与y轴相切时,x=3,
∴y=
| 6 |
| 3 |
∴点P的坐标是(2,3)或(3,2);
②当⊙P在第三象限,与x轴相切时,y=-3,
∴
| 6 |
| x |
解得x=-2,
与y轴相切时,x=-3,
∴y=
| 6 |
| -3 |
∴点P的坐标是(-2,-3)或(-3,-2).
综上所述,点P的坐标是(2,3)或(3,2)或(-2,-3)或(-3,-2).
故答案为:(2,3)或(3,2)或(-2,-3)或(-3,-2).
点评:此题主要考查了直线与圆相切的性质以及反比例函数图象上点的坐标性质,分情况把圆的半径的值看成点P的横坐标与纵坐标的值代入解析式求解是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 (2011•镇海区模拟)△OAB是直角三角形,∠AOB=30°,过A作AP⊥OB于P,在AP延长线上取一点C,使∠BOC=30°;过P作PQ⊥OC于P,在PQ延长线上取一点D,使∠COD=30°;…;按此方法操作,最终得到△OMN,此时ON在OA上.若AB=2a,则ON=
(2011•镇海区模拟)△OAB是直角三角形,∠AOB=30°,过A作AP⊥OB于P,在AP延长线上取一点C,使∠BOC=30°;过P作PQ⊥OC于P,在PQ延长线上取一点D,使∠COD=30°;…;按此方法操作,最终得到△OMN,此时ON在OA上.若AB=2a,则ON=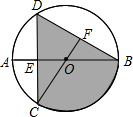 (2011•镇海区模拟)如图,已知⊙O的直径AB垂直于点E,连接CO并延长交BD于点F,若CF⊥BD,AB=8,
(2011•镇海区模拟)如图,已知⊙O的直径AB垂直于点E,连接CO并延长交BD于点F,若CF⊥BD,AB=8,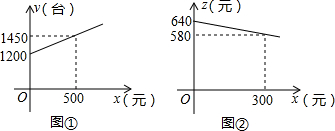 多少元?并求出总收益w的最大值.
多少元?并求出总收益w的最大值.