题目内容
 (2011•镇海区模拟)△OAB是直角三角形,∠AOB=30°,过A作AP⊥OB于P,在AP延长线上取一点C,使∠BOC=30°;过P作PQ⊥OC于P,在PQ延长线上取一点D,使∠COD=30°;…;按此方法操作,最终得到△OMN,此时ON在OA上.若AB=2a,则ON=
(2011•镇海区模拟)△OAB是直角三角形,∠AOB=30°,过A作AP⊥OB于P,在AP延长线上取一点C,使∠BOC=30°;过P作PQ⊥OC于P,在PQ延长线上取一点D,使∠COD=30°;…;按此方法操作,最终得到△OMN,此时ON在OA上.若AB=2a,则ON=4×(
)11a
| ||
| 2 |
4×(
)11a
.(可用式子表示)
| ||
| 2 |
分析:利用含30度角的直角三角形的性质,正三角形的性质和AB=2a,求得OP的长,然后逆时针旋转30°后可以求得OQ的长,直至线段ON与线段OA重合,一共旋转了12次,从而可以求得ON的长.
解答:解:∵∠A=90°,∠AOB=30°,AB=2a,
∴BO=4a,OC=OA=
×4a,
∵OP为等边三角形的高,且等边三角形的边长为
×4a,
∴OD=OP=(
)2×4a,
以此类推,当ON与OA重合时,一共旋转了12次,
∴ON的长为(
)11×4a=4×(
)11a.
故答案为:4×(
)11a.
∴BO=4a,OC=OA=
| ||
| 2 |
∵OP为等边三角形的高,且等边三角形的边长为
| ||
| 2 |
∴OD=OP=(
| ||
| 2 |
以此类推,当ON与OA重合时,一共旋转了12次,
∴ON的长为(
| ||
| 2 |
| ||
| 2 |
故答案为:4×(
| ||
| 2 |
点评:本题考查了含30度角的直角三角形的性质和正三角形的性质,解题的关键是正确地得到一共旋转了多少次.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 (2011•镇海区模拟)如图,半径为3的动圆⊙P,其圆心点P可在二支双曲线
(2011•镇海区模拟)如图,半径为3的动圆⊙P,其圆心点P可在二支双曲线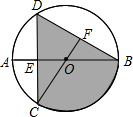 (2011•镇海区模拟)如图,已知⊙O的直径AB垂直于点E,连接CO并延长交BD于点F,若CF⊥BD,AB=8,
(2011•镇海区模拟)如图,已知⊙O的直径AB垂直于点E,连接CO并延长交BD于点F,若CF⊥BD,AB=8,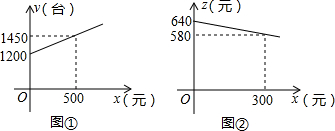 多少元?并求出总收益w的最大值.
多少元?并求出总收益w的最大值.