题目内容
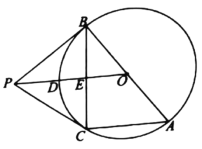
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 是
是![]() 的两条切线,切点分别为B,C.连接
的两条切线,切点分别为B,C.连接![]() 交
交![]() 于点D,交
于点D,交![]() 于点E,连接
于点E,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见详解;(2)![]() .
.
【解析】
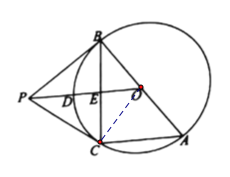
(1)连接OC,易证:RtPBO~RtPCO,根据等腰三角形三线合一,可得:OE是ABC的中位线,即可得证;
(2)由勾股定理得:![]() ,由母子相似三角形,可得:PO=
,由母子相似三角形,可得:PO=![]() ,进而求出PB的长.
,进而求出PB的长.
(1)连接OC,则OB=OC,
∵![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,
∴PB=PC,∠PBO=∠PCO=90°,
在RtPBO和RtPCO中,
∵![]() ,
,
∴RtPBO~RtPCO(HL),
∴∠BPO=∠CPO,
∴BE=CE(等腰三角形三线合一),
∴OE是ABC的中位线,
∴![]() ;
;
(2)∵OE是ABC的中位线,
∴OE∥AC,![]() ,
,
∴∠OEB=∠ACB=90°,
∵![]() ,
,
∵PB是圆的切线,
∴∠PBO=90°,
∵∠BOE=∠POB,
∴BOE~ POB,
∴![]() ,即:
,即:![]() ,
,
∴PO=![]() ,
,
∴![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目