题目内容
 如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC的D′处,AE是折痕.
如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC的D′处,AE是折痕.(1)图中有全等三角形吗?如果有,请写出来;
(2)求BD′的长;
(3)若设CE的长为x,请用含x的代数式表示线段D′E;
(4)求四边形ABCE的面积.
分析:(1)直接利用翻折变换的性质得出△ADE≌△AD′E;
(2)利用勾股定理得出BD′即可;
(3)利用CE的长为x,AB=DC=8,即可得出DE=D′E=8-x;
(4)利用以上所求利用勾股定理得出EC的长,进而利用梯形面积求出即可.
(2)利用勾股定理得出BD′即可;
(3)利用CE的长为x,AB=DC=8,即可得出DE=D′E=8-x;
(4)利用以上所求利用勾股定理得出EC的长,进而利用梯形面积求出即可.
解答: 解:(1)∵AD沿点A对折,点D正好落在BC的D′处,AE是折痕,
解:(1)∵AD沿点A对折,点D正好落在BC的D′处,AE是折痕,
∴△ADE≌△AD′E;
(2)∵△ADE≌△AD′E,
∴AD=AD′=10cm,
∵AB=8cm,
BD′=
=6(cm);
(3)∵设CE的长为x,AB=DC=8,
∴DE=D′E=8-x;
(4)设CE的长为x,AB=DC=8,DE=D′E=8-x,
∴在Rt△CD′E中,CD′=BC-BD′=10-6=4(cm),
∴(8-x)2=x2+42,
解得:x=3,
∴四边形ABCE的面积为:
×(AB+EC)×BC=
×10×(8+3)=55.
 解:(1)∵AD沿点A对折,点D正好落在BC的D′处,AE是折痕,
解:(1)∵AD沿点A对折,点D正好落在BC的D′处,AE是折痕,∴△ADE≌△AD′E;
(2)∵△ADE≌△AD′E,
∴AD=AD′=10cm,
∵AB=8cm,
BD′=
| AD′2-AB2 |
(3)∵设CE的长为x,AB=DC=8,
∴DE=D′E=8-x;
(4)设CE的长为x,AB=DC=8,DE=D′E=8-x,
∴在Rt△CD′E中,CD′=BC-BD′=10-6=4(cm),
∴(8-x)2=x2+42,
解得:x=3,
∴四边形ABCE的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了翻折变换的性质以及勾股定理等知识,利用翻折变换的性质得出EC的长是解题关键.

练习册系列答案
相关题目
 15、如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
15、如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
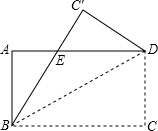 如图,在长方形纸片ABCD中,四个内角均为直角,AB=CD,AD=BC,将长方形纸片ABCD沿对角线BD进行折叠,点C的对称点为C′,BC′交AD于点E.
如图,在长方形纸片ABCD中,四个内角均为直角,AB=CD,AD=BC,将长方形纸片ABCD沿对角线BD进行折叠,点C的对称点为C′,BC′交AD于点E.