题目内容
 如图,∠1=75°,AB=BC=CD=DE=EF.则∠A的度数为
如图,∠1=75°,AB=BC=CD=DE=EF.则∠A的度数为
- A.30°
- B.20°
- C.25°
- D.15°
D
分析:已知AB=BC=CD=DE=EF,则可根据等腰三角形的性质得到几组相等的角,从而可推出∠EFD与∠A之间的关系,再根据三角形外角的性质即可求得∠A的度数.
解答:∵AB=BC=CD=DE=EF,
∴∠A=∠ACB,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD,
∴∠EFD=4∠A,
∵∠1=∠EFD+∠A=5∠A=75°,
∴∠A=15°.
故选D.
点评:此题主要考查学生对等腰三角形的性质及三角形外角的性质的综合运用.
分析:已知AB=BC=CD=DE=EF,则可根据等腰三角形的性质得到几组相等的角,从而可推出∠EFD与∠A之间的关系,再根据三角形外角的性质即可求得∠A的度数.
解答:∵AB=BC=CD=DE=EF,
∴∠A=∠ACB,∠CBD=∠CDB,∠DCE=∠DEC,∠EDF=∠EFD,
∴∠EFD=4∠A,
∵∠1=∠EFD+∠A=5∠A=75°,
∴∠A=15°.
故选D.
点评:此题主要考查学生对等腰三角形的性质及三角形外角的性质的综合运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
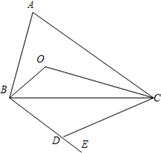 20、如图,∠A=75°,∠BOC=135°,∠ABO=∠CBE,∠ACO=∠BCD,则∠CDE=
20、如图,∠A=75°,∠BOC=135°,∠ABO=∠CBE,∠ACO=∠BCD,则∠CDE=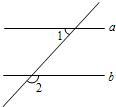 2、如图,∠1=75°,要使a∥b,则∠2等于( )
2、如图,∠1=75°,要使a∥b,则∠2等于( )
 如图,∠A=75°,则∠BOC=
如图,∠A=75°,则∠BOC=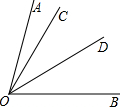 已知:如图,∠AOB=75°,∠AOC=15°,OD是∠BOC的平分线,求∠BOD的度数.
已知:如图,∠AOB=75°,∠AOC=15°,OD是∠BOC的平分线,求∠BOD的度数.