题目内容
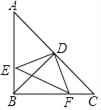
【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=![]() S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
根据ASA可证△BED≌△CFD,可得BE=CF,DE=DF,易证①AE=BF;②S四边形BEDF=![]() S△ABC;③△DEF是等腰直角三角形;由∠BFE=180-∠DFE-∠DFC,∠CDF=180-∠C-∠DFC, ∠DFE=∠C得∠BFE=∠CDF.
S△ABC;③△DEF是等腰直角三角形;由∠BFE=180-∠DFE-∠DFC,∠CDF=180-∠C-∠DFC, ∠DFE=∠C得∠BFE=∠CDF.
∵ED⊥FD,BD⊥AC,
∴∠BDE+∠BDF=90°,∠BDF+∠FDC=90°,
∴∠BDE=∠FDC,
∵△ABC为等腰直角三角形,BD⊥AC,
∴∠EBD=∠C=45°,BD=CD,
在△BED和△CFD中,
 ,
,
∴△BED≌△CFD(ASA),
∴BE=CF,
∴AE=BF,选项①正确;
DE=DF,
∴△DEF为等腰直角三角形,选项③正确;
∴S四边形BEDF=S△BED+S△BDF=S△CFD+S△BDF=S△BDC=![]() S△ABC,选项②正确.
S△ABC,选项②正确.
∵∠BFE=180-∠DFE-∠DFC,∠CDF=180-∠C-∠DFC, ∠DFE=∠C=45,
∴∠BFE=∠CDF,选项④正确;
上述结论中始终成立的有4个.
故选:D

【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 ![]() =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③