题目内容
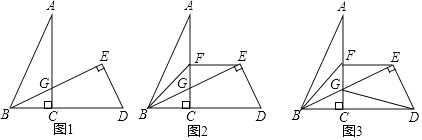
【题目】如图 1,直线![]() 分别交
分别交![]() 于点
于点![]() (点
(点![]() 在点
在点![]() 的右侧),若
的右侧),若![]()
(1)求证:![]() ;
;

(2)如图2所示,点![]() 在
在![]() 之间,且位于
之间,且位于![]() 的异侧,连
的异侧,连![]() , 若
, 若![]() ,则
,则![]() 三个角之间存在何种数量关系,并说明理由.
三个角之间存在何种数量关系,并说明理由.

(3)如图 3 所示,点![]() 在线段
在线段![]() 上,点
上,点![]() 在直线
在直线![]() 的下方,点
的下方,点![]() 是直线
是直线![]() 上一点(在
上一点(在![]() 的左侧),连接
的左侧),连接![]() ,若
,若![]() ,则请直接写出
,则请直接写出![]() 与
与![]() 之间的数量
之间的数量

【答案】(1)证明过程见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ∠N+∠PMH=180°.
∠N+∠PMH=180°.
【解析】
(1)根据同旁内角互补,两直线平行即可判定AB∥CD;
(2)设∠N=![]() ,∠M=
,∠M=![]() ,∠AEM=
,∠AEM=![]() ,∠NFD=
,∠NFD=![]() ,过M作MP∥AB,过N作NQ∥AB可得∠PMN=
,过M作MP∥AB,过N作NQ∥AB可得∠PMN=![]() -
-![]() ,∠QNM=
,∠QNM=![]() -
-![]() ,根据平行线性质得到
,根据平行线性质得到![]() -
-![]() =
=![]() -
-![]() ,化简即可得到
,化简即可得到![]() ;
;
(3)过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R,根据平行线的性质可得∠BPM=∠PMI,由已知得到∠MON=∠MPN+∠PMI=3∠PMI及∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD,根据对顶角相等得到∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM,化简得到∠FNP+2∠PMI-2∠RFM=180°-∠PMH,根据平行线的性质得到3∠PMI+∠FNP+∠FNH=180°及3∠RFM+∠FNH=180°,两个等式相减即可得到∠RFM-∠PMI=![]() ∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到
∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到![]() ∠FNP=180°-∠PMH,即
∠FNP=180°-∠PMH,即![]() ∠N+∠PMH=180°.
∠N+∠PMH=180°.
(1)证明:∵∠1=∠BEF,![]()
∴∠BEF+∠2=180°
∴AB∥CD.
(2)解:![]()
设∠N=![]() ,∠M=
,∠M=![]() ,∠AEM=
,∠AEM=![]() ,∠NFD=
,∠NFD=![]()
过M作MP∥AB,过N作NQ∥AB
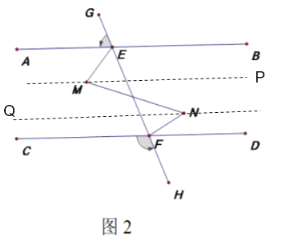
∵![]() ,MP∥AB,NQ∥AB
,MP∥AB,NQ∥AB
∴MP∥NQ∥AB∥CD
∴∠EMP=![]() ,∠FNQ=
,∠FNQ=![]()
∴∠PMN=![]() -
-![]() ,∠QNM=
,∠QNM=![]() -
-![]()
∴![]() -
-![]() =
=![]() -
-![]()
即![]() =
=![]() -
-![]()
∴![]()
故答案为![]()
(3)解:![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R.
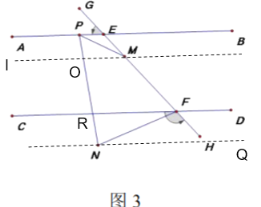
∵![]() ,MI∥AB,NQ∥CD
,MI∥AB,NQ∥CD
∴AB∥MI∥NQ∥CD
∴∠BPM=∠PMI
∵∠MPN=2∠MPB
∴∠MPN=2∠PMI
∴∠MON=∠MPN+∠PMI=3∠PMI
∵∠NFH=2∠HFD
∴∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD
∵∠RFN=∠HFD
∴∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM
∴∠MON+∠PRF+∠RFM=360°-∠OMF
即3∠PMI+∠FNP+180°-3∠RFM+∠RFM=360°-∠OMF
∴∠FNP+2∠PMI-2∠RFM=180°-∠PMH
∵3∠PMI+∠PNH=180°
∴3∠PMI+∠FNP+∠FNH=180°
∵3∠RFM+∠FNH=180°
∴3∠PMI-3∠RFM+∠FNP=0°
即∠RFM-∠PMI=![]() ∠FNP
∠FNP
∴∠FNP+2∠PMI-2∠RFM=∠FNP-2(∠RFM-∠PMI)=180°-∠PMH
∠FNP-2×![]() ∠FNP=180°-∠PMH
∠FNP=180°-∠PMH
![]() ∠FNP=180°-∠PMH
∠FNP=180°-∠PMH
即![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
故答案为![]() ∠N+∠PMH=180°
∠N+∠PMH=180°

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案