题目内容
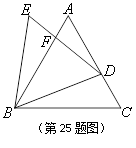
如图,已知![]() 与
与![]() 都是等边三角形,点
都是等边三角形,点![]() 在边
在边![]() 上(不与
上(不与![]() 、
、![]() 重合),
重合),![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
(2)若![]() ,设
,设![]() ,
,![]() ;
;
①求![]() 关于
关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
②当![]() 为何值时,
为何值时,![]() ?
?
(1)证明略
(2)
①![]()
②当![]() 或
或![]() 时,
时,![]()
解析:(1)证明:∵![]() 与
与![]() 都是等边三角形,
都是等边三角形,
∴![]() ,……………………………………………………(1分)
,……………………………………………………(1分)
∵![]() ,∴
,∴![]() ,……………………(2分)
,……………………(2分)
∴![]() ∽
∽![]() .………………………………………………………………(1分)
.………………………………………………………………(1分)
(2)∵![]() ∽
∽![]() ,∴
,∴![]() ,………………………………………(1分)
,………………………………………(1分)
∵![]() ,设
,设![]() ,
,![]() ,∴
,∴![]() ,………………………………(1分)
,………………………………(1分)
∴![]() .……………………………………………………………(2分)
.……………………………………………………………(2分)
(3)解法一:∵![]() 与
与![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() ,∴
,∴![]() ,…………(1分)
,…………(1分)
∴![]() ∽
∽![]() ,∴
,∴![]() ,……………………………………………(1分)
,……………………………………………(1分)
∵![]() ,
,![]() ,∴
,∴![]() ,……………………………………………(1分)
,……………………………………………(1分)
∵![]() ∽
∽![]() ,
,![]() ,∴
,∴![]() ,……………………(1分)
,……………………(1分)
∴![]() ,∴
,∴![]() ,…………………………………………………(1分)
,…………………………………………………(1分)
∴![]() ,解得
,解得![]() ,∴当
,∴当![]() 或
或![]() 时,
时,![]() .…………(1分)
.…………(1分)
解法二:∵△ABC与![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() ,∴
,∴![]() ,…………(1分)
,…………(1分)
∴![]() ∽
∽![]() ,∵
,∵![]() ,∴
,∴![]() ,……………………(1分)
,……………………(1分)
∵![]() ,
,![]() ,∴
,∴![]() . ……………………………………………(1分)
. ……………………………………………(1分)
过点![]() 作
作![]() 于点
于点![]() ,……………………………………………………(1分)
,……………………………………………………(1分)
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,
当点![]() 在线段
在线段![]() 上时,
上时,![]() ;………………………(1分)
;………………………(1分)
当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ,……………(1分)
,……………(1分)
综上所述,当![]() 或
或![]() 时,
时,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
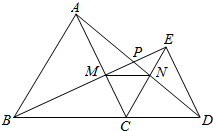 已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( ) 与
与 都是等边三角形,点
都是等边三角形,点 在边
在边 上(不与
上(不与 、
、 重合),
重合), 与
与 相交于点
相交于点 .
.
 ∽
∽ ;
; ,设
,设 ,
, ;
; 关于
关于 的函数解析式及定义域;
的函数解析式及定义域; ?
?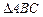 与
与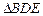 都是等边三角形,点
都是等边三角形,点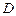 在边
在边 上(不与
上(不与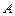 、
、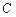 重合),
重合),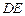 与
与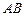 相交于点
相交于点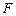 .
.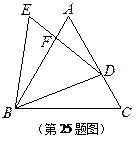

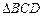 ∽
∽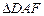 ;
;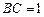 ,设
,设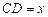 ,
,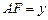 ;
;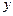 关于
关于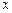
 的函数解析式及定义域;
的函数解析式及定义域;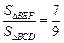 ?
?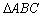 与
与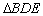 都是等边三角形,点
都是等边三角形,点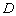 在边
在边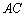 上(不与
上(不与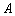 、
、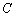 重合),
重合),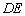 与
与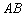 相交于点
相交于点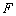 .
.
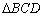 ∽
∽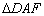 ;
;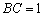 ,设
,设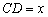 ,
,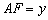 ;
;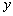 关于
关于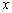 的函数解析式及定义域;
的函数解析式及定义域;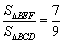 ?
?