题目内容
(6分)如图,线段 经过圆心
经过圆心 ,交⊙O于点
,交⊙O于点 ,点
,点 在⊙O上,连接
在⊙O上,连接 ,∠A=∠B=30°.
,∠A=∠B=30°.

证明:(1)BD是⊙O的切线
(2)如果BD=2求OC的长
(1)见解析 (2)
【解析】
试题分析:(1)连接OD,根据∠A和∠B的度数求出∠ADB的度数,然后根据OA=OD求出∠ODA的度数,从而可以得到∠ODB的度数;(2)根据△BOD为直角三角形和BD的长度,求出OD的长度,然后OC=OD求出OC的长度.
试题解析:(1)连接OD ∵OA=OD ∴∠ODA=∠A=30°
∵∠A=∠B=30° ∴∠ADB=180°-30°-30°=120° ∴∠ODB=120°-30°=90°
∴BD是⊙O的切线.
(2)∵∠BDO=90° ∠B=30° BD=2 ∴OD= ∴OC=OD=
∴OC=OD= .
.
考点:圆的切线的证明、等腰三角形的性质.

练习册系列答案
相关题目
 2cos60°+
2cos60°+
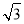 ,坝高BC=10m,则坡面AB的长度是( )
,坝高BC=10m,则坡面AB的长度是( )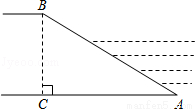
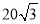 m C.
m C.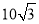 m D.20m
m D.20m ,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-12x+32=O的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-12x+32=O的两根.
 -
- =1的解为负数,则a的取值范围是 .
=1的解为负数,则a的取值范围是 . +
+ =0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
=0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。