题目内容
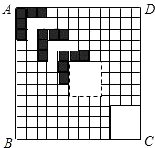
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n﹣1)×(n﹣1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
请你认真观察思考后回答下列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸片的张数也不同,请填写下表:
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 | __________ | __________ | __________ | __________ | __________ |
(2)设正方形ABCD被纸片盖住的面积(重合部分只计一次)为S1,未被盖住的面积为S2.
①当n=2时,求S1:S2的值;
②用含n的代数式表示S2.
【考点】规律型:图形的变化类.
【分析】(1)根据题意,可得应盖住正方形ABCD的对角线上的12个格.当是边长为2的纸片时,则需要1+(12﹣2)=11张纸片.当边长为3的时候,则需要1+(12﹣3)=10张纸片.当边长为44时,则需要1+(12﹣4)=9张纸片,依此类推进行计算即可;
(2)①第一个面积为n2,第二个为一个包边,共有12﹣n个,每个由2n﹣1个小正方形构成,包边的总面积为(12﹣n)×(2n﹣1),由此得出S1=(12﹣n)×(2n﹣1)+n2;S2=144﹣(12﹣n)×(2n﹣1)﹣n2,代入计算得出答案即可;
②由①得出答案即可.
【解答】解:(1)填表如下
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 | 11 | 10 | 9 | 8 | 7 |
(2)∵第一个面积为n2,第二个为一个包边,共有12﹣n个,每个由2n﹣1个小正方形构成,包边的总面积为(12﹣n)×(2n﹣1)
∴①S1=10×3+4=34,S2=144﹣34=110.
∴S1:S2的值是34:110=17:55.
②根据题意,S2=144﹣(12﹣n)×(2n﹣1)﹣n2,、.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 的倒数是__________.
的倒数是__________. 的值是( )
的值是( ) 的系数是__________;
的系数是__________;