题目内容
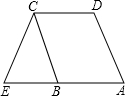如图，AD∥BC，点E在的延长线上，CB=CE，试说明∠A=∠E．
证明：∵CB=CE
∴∠E=CBE
又∵AD∥BC
∴∠A=∠CBE
∴∠A=∠E．
分析：本题可把证明∠A=∠E的问题可以转化为同一个三角形的角，边的关系来求解．
点评：本题主要考查了等腰三角形的性质；将所求的条件转化为同一个三角形的角，边的关系是解题的基本思路．
∴∠E=CBE
又∵AD∥BC
∴∠A=∠CBE
∴∠A=∠E．
分析：本题可把证明∠A=∠E的问题可以转化为同一个三角形的角，边的关系来求解．
点评：本题主要考查了等腰三角形的性质；将所求的条件转化为同一个三角形的角，边的关系是解题的基本思路．
练习册系列答案
相关题目
25、如图，AD⊥BC于点D，∠1=2，∠CDG=∠B，请你判断EF与BC的位置关系，并加以证明，要求写出每步证明的理由．
11、如图，AD∥BC，点E在BD的延长线上，若∠ADE=155°，则∠DBC=
98、如图，AD∥BC，点E在的延长线上，CB=CE，试说明∠A=∠E．
如图，AD⊥BC于点D，∠1=∠2，∠CDG=∠B，试说明EF⊥BC的理由．
如图，AD∥BC，点O在AD上，BO，CO分别平分∠ABC，∠DCB，若∠A+∠D=246°．