题目内容
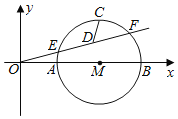
【题目】如图,点![]() 是
是![]() 的内心,
的内心,![]() 的延长线和
的延长线和![]() 的外接圆相交于点
的外接圆相交于点![]() ,交
,交![]() 于
于![]() .
.
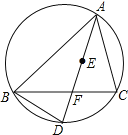
(1)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)30°;(2)见解析;(3)![]()
【解析】
(1)由三角形的内心定义和同弧所对的圆周角相等即可解答;
(2)连接BE,根据三角形的内心定义和同弧所对的圆周角相等证得∠DBE=∠BED,从而依据等角对等边即可证得;
(3)利用已知和角平分线的性质得![]() ,进而求得BF、CF的值,再证明△BDF∽△ACF和△DBF∽△DAB,利用相似三角形的性质得到关于BD的方程,解之即可解答﹒
,进而求得BF、CF的值,再证明△BDF∽△ACF和△DBF∽△DAB,利用相似三角形的性质得到关于BD的方程,解之即可解答﹒
(1)∵![]() ,
,![]() ,
,
∴∠BAC=180-∠ABC-∠C=60,
∵E是内心,
∴∠BAD=∠CAD=![]() ∠BAC=30,
∠BAC=30,
由同弧所对的圆周角相等得:
∠CBD=∠CAD=30;
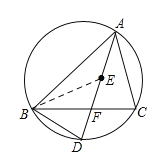
(2)证明:连接BE,
∵E是内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠CBD=∠CAD,
∴∠CBD=∠BAD,
∵∠BAD+∠ABE=∠BED,∠CBE+∠CBD=∠DBE,
∴∠DBE=∠BED,
∴ DE=DB;
(3)∵∠BAD=∠CAD,AB=6,AC=4,BC=5
∴![]()
∴ BF=3,CF=2
∵∠DBC=∠DAC,∠BFD=∠AFC
∴ △BDF∽△ACF
∴![]() ,
,
∴![]() ,
,
∵∠BAD=∠CAD=∠DBC,∠BDF=∠ADB
∴ △DBF∽△DAB
∴![]() ,
,
∴![]() ,
,
∴![]() ,又BD=DE,
,又BD=DE,
∴![]() .
.

练习册系列答案
相关题目