题目内容
在正方形ABCD的边BC的延长线上取一点E，使CE=AC，AE与CD交于点F，那么∠AFC的度数为
- A.105°
- B.112.5°
- C.135°
- D.120°
B
分析：根据正方形的性质，得∠ACB=∠2=45°，根据等腰三角形的性质和三角形的外角的性质，得∠1=∠E=22.5°，从而根据三角形的内角和定理进行计算．
解答：
解：∵四边形ABCD是正方形，
∴∠ACB=∠2=45°．
∵AC=CE，
∴∠1=∠E=22.5°．
∴∠AFC=180°-45°-22.5°=112.5°．
故选B．
点评：此题综合运用了正方形的性质、三角形的内角和定理及其推论、等腰三角形的性质．
分析：根据正方形的性质，得∠ACB=∠2=45°，根据等腰三角形的性质和三角形的外角的性质，得∠1=∠E=22.5°，从而根据三角形的内角和定理进行计算．
解答：
解：∵四边形ABCD是正方形，∴∠ACB=∠2=45°．
∵AC=CE，
∴∠1=∠E=22.5°．
∴∠AFC=180°-45°-22.5°=112.5°．
故选B．
点评：此题综合运用了正方形的性质、三角形的内角和定理及其推论、等腰三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
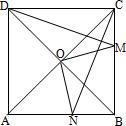42、如图，在正方形ABCD的边BC上任取一点M，过点C作CN⊥DM交AB于N，设正方形对角线交点为O，试确定OM与ON之间的关系，并说明理由．
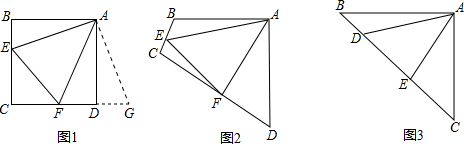
如图，正方形CEFG的对角线CF在正方形ABCD的边BC的延长线上（CE＞BC），点M在CF上，且MF=AB，线段AF与DM交于点N．