题目内容
一张长方形桌子可坐6人,2张桌子拼在一起可坐8人,按如图方式讲桌子拼在一起.
那么3张桌子拼在一起可坐 人,n张桌子拼在一起可坐 人.

那么3张桌子拼在一起可坐
考点:规律型:图形的变化类
专题:
分析:根据图形查出2张桌子,3张桌子可坐的人数,然后得出每多一张桌子可多坐2人的规律,然后解答.
解答:解:①由图可知,2张桌子拼在一起可坐8人,
3张桌子拼在一起可坐10人,
…
依此类推,每多一张桌子可多坐2人,
所以,n张桌子拼在一起可坐2n+4;
故答案为:10;2n+4.
3张桌子拼在一起可坐10人,
…
依此类推,每多一张桌子可多坐2人,
所以,n张桌子拼在一起可坐2n+4;
故答案为:10;2n+4.
点评:本题是对图形变化规律的考查,根据图形,观察得出每多一张桌子可多坐2人的规律并求出n张桌子可坐的人数的表达式是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
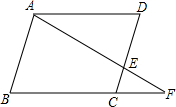 如图:在平行四边形ABCD中,AF交DC于E,交BC的延长线于F,若
如图:在平行四边形ABCD中,AF交DC于E,交BC的延长线于F,若 如图,MN是圆柱底面的直径,MN=2,MP是圆柱的高,MP=4,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,则金属丝的长为
如图,MN是圆柱底面的直径,MN=2,MP是圆柱的高,MP=4,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,则金属丝的长为