题目内容
如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；
求证：BC=DC．
考点：
全等三角形的判定与性质．
专题：
证明题．
分析：
先求出∠ACB=∠ECD，再利用“角边角”证明△ABC和△EDC全等，然后根据全等三角形对应边相等证明即可．
解答：
证明：∵∠BCE=∠DCA，
∴∠BCE+∠ACE=∠DCA+∠ACE，
即∠ACB=∠ECD，
在△ABC和△EDC中，
，
∴△ABC≌△EDC（ASA），
∴BC=DC．
点评：
本题考查了全等三角形的判定与性质，求出相等的角∠ACB=∠ECD是解题的关键，也是本题的难点．
练习册系列答案
名校课堂系列答案
相关题目
9、如图，已知EB=EC，要使△ABC≌△DCB，还必须增加条件，现在给出下列三个条件：①∠ABC=∠DCB；②∠A=∠D；③AE=DE，那么可以作为增加条件的有（ ）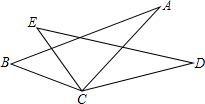
（2013•平凉）如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为
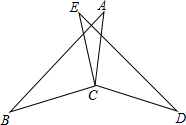（2013•珠海）如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；
如图，已知BC=EC，∠BCE=∠ACD，添加一个条件，使△ABC≌△DEC，你添加的条件是