题目内容
(1)若
=
=
,求
的值.
(2)已知二次函数图象与x轴交点(2,0),(-1,0),与y轴交点是(0,-1),求此二次函数解析式.
| a |
| 5 |
| b |
| 7 |
| c |
| 8 |
| 2a+b+3c |
| 2a-b+3c |
(2)已知二次函数图象与x轴交点(2,0),(-1,0),与y轴交点是(0,-1),求此二次函数解析式.
分析:(1)设
=
=
=k,然后用k分别表示a、b、c的值,将它们代入所求的代数式
消去k即可得到
的值;
(2)可设二次函数的解析式为两点式:y=a(x-2)(x+1)(a≠0),然后将点(0,-1)代入该函数解析式即可求得a的值.
| a |
| 5 |
| b |
| 7 |
| c |
| 8 |
| 2a+b+3c |
| 2a-b+3c |
| 2a+b+3c |
| 2a-b+3c |
(2)可设二次函数的解析式为两点式:y=a(x-2)(x+1)(a≠0),然后将点(0,-1)代入该函数解析式即可求得a的值.
解答:解:(1)设
=
=
=k,则a=5k,b=7k,c=8k.
当k=0时,即a=b=c=0,则2a-b+3c=0,分式
无意义,故k≠0.
所以
=
=
=
,即
=
;
(2)∵二次函数图象与x轴交点(2,0),(-1,0),
∴设二次函数的解析式为:y=a(x-2)(x+1)(a≠0),
又∵二次函数图象与y轴交点是(0,-1),
∴-1=a(0-2)(0+1),即-1=-2a,
解得,a=
,
∴该二次函数的解析式为y=
(x-2)(x+1),或y=
x2-
x-1.
| a |
| 5 |
| b |
| 7 |
| c |
| 8 |
当k=0时,即a=b=c=0,则2a-b+3c=0,分式
| 2a+b+3c |
| 2a-b+3c |
所以
| 2a+b+3c |
| 2a-b+3c |
| 2×5k+7k+3×8k |
| 2×5k-7k+3×8k |
| 41k |
| 27k |
| 41 |
| 27 |
| 2a+b+3c |
| 2a-b+3c |
| 41 |
| 27 |
(2)∵二次函数图象与x轴交点(2,0),(-1,0),
∴设二次函数的解析式为:y=a(x-2)(x+1)(a≠0),
又∵二次函数图象与y轴交点是(0,-1),
∴-1=a(0-2)(0+1),即-1=-2a,
解得,a=
| 1 |
| 2 |
∴该二次函数的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了比例的性质,待定系数法求二次函数的解析式.二次函数的解析式由三种形式,解答该题时根据已知条件设解析式的形式为两点式.

练习册系列答案
相关题目
若
=
=
,且3a-2b+c=3,则2a+4b-3c的值是( )
| a |
| 5 |
| b |
| 7 |
| c |
| 8 |
| A、14 | ||
| B、42 | ||
| C、7 | ||
D、
|
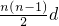 ,求:
,求: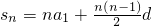 计算:3,5,7,9,11,13,…103这几个数的和.
计算:3,5,7,9,11,13,…103这几个数的和.