题目内容

精英家教网D、E分别是△ABC的边AB、AC的中点，
AB
=
a
，
AC
=
b
，则
DE
等于（　　）
A、
1
2
(
a
+
b
)
B、
1
2
(
a
-
b
)
C、
1
2
(
b
-
a
)
D、-
1
2
(
a
+
b
)
分析：首先由D、E分别是△ABC的边AB、AC的中点，可得DE∥BC，DE=
1
2
BC，然后由
BC
=
AC
-
AB
，即可求得答案．
解答：解：∵D、E分别是△ABC的边AB、AC的中点，
∴DE∥BC，DE=
1
2
BC，
∴
DE
=
1
2
BC
，
∵
AB
=
a
，
AC
=
b
，
∴
BC
=
AC
-
AB
=
b
-
a
，
∴
DE
=
1
2
（
b
-
a
）．
故选C．
点评：此题考查了平面向量的知识与三角形中位线的性质．解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
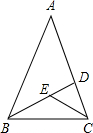精英家教网如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（　　）
A、5个B、4个C、3个D、2个
精英家教网如图所示，已知点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，FG=1，则CF的长为（　　）
A、2B、1.5C、3D、4
16、如图，D，E分别是△ABC的边CA、BA的延长线上的点，请你添加一个条件，使△ADE与△ABC相似．你添加的条件是
∠ADE=∠ABC或AD：AC=AE：AB等（答案不唯一）
．
如图，点D，E，F分别是△ABC（AB＞AC）各边中点，下列说法不正确的是（　　）
如图，在六边形ABCDEF中，BA⊥FA，BC⊥DC，∠α、∠β分别是∠ABC和∠EDC的补角，∠α=55°，∠β=30°，则∠E+∠F的度数为
265°
265°
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网