题目内容
2.如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.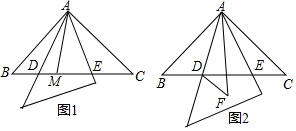
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了相同的方法进行解决:将△ABD沿AD所在的直线对折得到△ADF(如图2);请证明小敏的发现的是正确的.
分析 (1)根据图形、已知条件推知∠BAD+∠MAE=∠DAM+∠EAC=45°,所以∠MAE=∠EAC,即AE平分∠MAC;
(2)应用折叠对称的性质和SAS得到△AEF≌△AEC,在Rt△OCE中应用勾股定理而证明;
解答 解:(1)证明:∵∠BAC=90°,
∴∠BAD+∠DAM+∠MAE+∠EAC=90°.
∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∵∠BAD=∠DAM,
∴∠BAD+∠EAC=∠DAM+∠EAC=45°,
∴∠BAD+∠MAE=∠DAM+∠EAC,
∴∠MAE=∠EAC,
即AE平分∠MAC;
(2)如图2,
连接EF.
由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,$\left\{\begin{array}{l}{AF=AC}\\{∠FAE=∠CAE}\\{AE=AE}\end{array}\right.$
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2.
点评 此题是几何变换综合题,主要考查了角平分线的定义,等腰直角三角形的性质,旋转的性质,折叠对称的性质,全等三角形的判定和性质等知识点.注意,旋转前后,图形的大小和形状都不改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.抛物线y=-2(x-1)2-3的最大值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
7.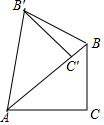 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠C′B′B的度数为( )| A. | 40° | B. | 20° | C. | 70° | D. | 50° |

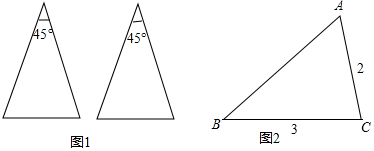
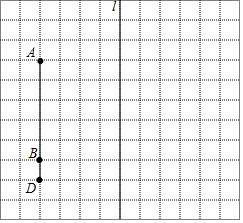 如图,在正方形网格中,每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上,点B是线段AD上的格点,且BD=1,直线l在格线上.
如图,在正方形网格中,每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上,点B是线段AD上的格点,且BD=1,直线l在格线上.