题目内容
数学兴趣小组成员,为了从一张腰长为2的等腰直角三角形的纸片中剪出一个尽可能大的正方形,探究出甲、乙两种剪法(图甲、图乙)
(1)请计算说明甲、乙两种解法哪种剪出的正方形纸片更大.
(2)李明同学想从一张直角边分别为3、4的三角形纸片中,剪出一个边长为1.7的正方形能做到吗?若能,请说明理由,并在图中用虚线画出所剪正方形;若不能,请说明不能的理由.

解:(1)如图甲所示:设正方形的边长为x,则AE=2-x,
∵DE⊥AC,BC⊥AC,
∴△ADE∽△ABC,
∴ =
= ,
,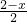 =
= ,
,
解得x=1,
∴S正方形=1;
如图乙所示:
∵等腰直角三角形的边长为2,
∴AB= =
= =2
=2 ,
,
设正方形的边长为x,则AD= =
= -
- ,
,
∵∠A=∠A,∠ADE=∠ACB,
∴△ADE∽△ACB,
∴ =
= ,
, =
= ,
,
解得x=
∴S正方形=( )2=
)2= ;
;
∵1> ,
,
∴甲种剪法面积更大;

(2)能.
如图丙所示:
设正方形的边长为x,则AE=3-x,
∵DE⊥AC,BC⊥AC,
∴△ADE∽△ABC,
∴ =
= ,
,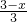 =
= ,
,
解得x= ≈1.71>1.7,
≈1.71>1.7,
∴剪出一个边长为1.7的正方形.
分析:(1)设正方形的边长为x,再根据相似三角形的性质计算出其边长,并比较出其大小即可;
(2)设正方形的边长为x,则AE=3-x,根据DE⊥AC,BC⊥AC,故可得出△ADE∽△ABC,再根据相似三角形的对应边成比例即可求出x的值,再与1.7相比较即可.
点评:本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
∵DE⊥AC,BC⊥AC,
∴△ADE∽△ABC,
∴
 =
= ,
,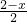 =
= ,
,解得x=1,
∴S正方形=1;
如图乙所示:
∵等腰直角三角形的边长为2,
∴AB=
 =
= =2
=2 ,
,设正方形的边长为x,则AD=
 =
= -
- ,
,∵∠A=∠A,∠ADE=∠ACB,
∴△ADE∽△ACB,
∴
 =
= ,
, =
= ,
,解得x=

∴S正方形=(
 )2=
)2= ;
;∵1>
 ,
,∴甲种剪法面积更大;

(2)能.
如图丙所示:
设正方形的边长为x,则AE=3-x,
∵DE⊥AC,BC⊥AC,
∴△ADE∽△ABC,
∴
 =
= ,
,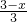 =
= ,
,解得x=
 ≈1.71>1.7,
≈1.71>1.7,∴剪出一个边长为1.7的正方形.
分析:(1)设正方形的边长为x,再根据相似三角形的性质计算出其边长,并比较出其大小即可;
(2)设正方形的边长为x,则AE=3-x,根据DE⊥AC,BC⊥AC,故可得出△ADE∽△ABC,再根据相似三角形的对应边成比例即可求出x的值,再与1.7相比较即可.
点评:本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
小明在“五•一”长假期间跟随父母去著名风景区旅游,小明是数学兴趣小组成员,在登山时,他做了一个实验:用自带的温度计与高度计,测量山上的高度与温度,每登高100m,他就测量一下温度,结果他得到如下的数据问:
| 高度计测得高度 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| 温度(℃) | 23.5 | 22.84 | 22.18 | 21.52 | 20.86 | 20.2 | 19.54 | 18.88 |
(2)从表中可以看出随着山的高度的升高,温度怎样变化?
(3)高度每升高100m,温度的变化相同吗?
(4)请你估计一下,当高度是2000m时,温度会是多少?你是怎样估计的?
(5)小明爬到某一高度后,开始感觉到比较冷(约为11.62℃),请问此时高度约为多少?你是怎样算的?

 请你根据图表提供的信息,解答下列问题:
请你根据图表提供的信息,解答下列问题: