题目内容

24、阅读下列材料，然后回答文后问题．
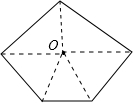
如图，在n边形内任取一点O，并把O与各顶点连接起来，共构成n个三角形，这n个三角形的内角和为n•180°，再减去以点O为顶点的一个周角，就可以得到n边形的内角和为（n-2）•180°．
回答：
（1）这种方法是将
多边形
问题转化为
三角形
问题来解决的，这种转化是
化归
思想的体现，也正是解决
多边形
问题的基本思想；
（2）若在n边形的一边上或外部任取一点O，并把O与各顶点连接起来，那么如何说明n边形的内角和为（n-2）•180°．
分析：（1）根据解决多边形问题的基本思想求解；
（2）若在n边形的一边上或外部任取一点O，并把O与各顶点连接起来，那么共构成（n-1）个三角形，此n边形的内角和为这（n-1）个三角形的内角和减去180°，从而得出结论．
解答：解：（1）多边形，三角形，化归，多边形；

（2）若O在一边上，连接O与各顶点，则共构成（n-1）个三角形，这（n-1）个三角形的内角和为（n-1）•180°，再减去以点O为顶点的一个平角，即（n-1）•180°-180°=（n-2）•180°；若点O在外部，同样也可说明．
点评：本题主要考查了n边形的内角和定理的推导，体现了数学中的划归思想．
练习册系列答案
相关题目
阅读下列材料，然后回答问题．
在进行二次根式运算时，形如
2
3
-1
一样的式子，我们可以将其进一步化简：
2
3
-1
=
2×(
3
+1)
(
3
-1)(
3
+1)
=
2(
3
+1)
3-1
=
3
+1
以上这种化简的步骤叫做分母有理化．
（1）请用上述的方法化简
2
5
-
3
；
（2）化简：
4
2
+2
+
4
2+
6
+
4
6
+
8
+…+
4
2n
+
2n+2
．
阅读下列材料，然后回答问题．
在进行二次根式计算时，我们有时会碰到如
5
3
，
2
3
，
2
3
+1
一样的式子，其实我们还可以将其进一步简化：
5
3
=
5×
3
3
×
3
=
5
3
3
          ①
2
3
=
2×3
3×3
=
6
3
             ②
2
3
+1
=
2(
3
-1)
(
3
+1)(
3
-1)
=
2(
3
-1)
(
3
)2-
1
2
 
=
2(
3
-1)
2
=
3
-1      ③
以上这种化简的步骤叫做分母有理化，
2
3
+1
还可以用以下方法化简：
2
3
+1
=
3-1
3
+1
=
(
3
)2-12
3
+1
=
3
-1     ④
（1）请用不同的方法化简：
2
7
+
5

参照③式方法化简过程为：
参照④式方法化简过程为：
（2）化简：
2
3
+1
+
2
5
+
3
+
2
7
+
5
+…+
2
2n+1
+
2n-1
．
（2012•香洲区一模）阅读下列材料，然后回答问题：
在进行类似于二次根式
2
3
+1
的运算时，通常有如下两种方法将其进一步化简：
方法一：
2
3
+1
=
2(
3
-1)
(
3
+1)(
3
-1) 
=
2(
3
-1)
(
3
)2- 1
=
3
-1
方法二：
2
3
-1
=
3-1
3
+1
=
(
3
)2-1
3
+1
=
(
3
+1)(
3
-1) 
3
+1
=
3
-1
（1）请用两种不同的方法化简：
2
5
+
3
 
；
（2）化简：
1
4
+
2
+
1
6
+
4
+ 
1
8
+
6
+…+
1
2012
+
2010
．

阅读下列材料，然后回答文后问题．
如图，在n边形内任取一点O，并把O与各顶点连接起来，共构成n个三角形，这n个三角形的内角和为n•180°，再减去以点O为顶点的一个周角，就可以得到n边形的内角和为（n-2）•180°．
回答：
（1）这种方法是将______问题转化为______问题来解决的，这种转化是______思想的体现，也正是解决______问题的基本思想；
（2）若在n边形的一边上或外部任取一点O，并把O与各顶点连接起来，那么如何说明n边形的内角和为（n-2）•180°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网