题目内容
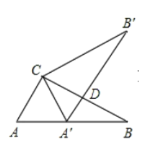
【题目】如图1,三角形纸片![]() ,先将该纸片沿过点
,先将该纸片沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在斜边
落在斜边![]() 上的一点
上的一点![]() 处,折痕记为
处,折痕记为![]() (如图1).剪去
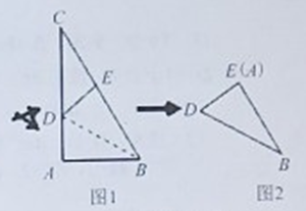
(如图1).剪去![]() 后得到双层
后得到双层![]() (如图2),再沿着过
(如图2),再沿着过![]() 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为______
某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为______![]()
【答案】![]() 或
或![]()
【解析】
首先根据折叠及勾股定理求出DE的长,再分两种情况,①如图2中,当ED=EF时,②如图2-1中,当FD=FB时,分别求解即可解决问题.
解:如图1中,∵∠A=90°,∠C=30°,AC=8cm,
∴AB=BE=![]() ,BC=2AB=
,BC=2AB=![]() ,
,
∴CE=BC-BE=![]()
设AD=DE=x,
则在Rt△CDE中,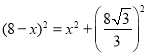 ,
,
解得x=![]() ,即DE=
,即DE=![]() ,
,
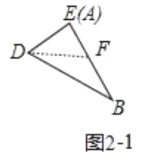
①如图2中,当ED=EF时,沿着直线EF将双层三角形剪开,展开后的平面图形中有一个是平行四边形,此时周长=![]() cm
cm

②如图2-1中,当FD=FB时,沿着直线DF将双层三角形剪开,展开后的平面图形中有一个是平行四边形,此时周长=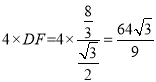 cm
cm
综上所述,所得平行四边形的周长为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]()

练习册系列答案
相关题目
【题目】我市某工艺厂设计了款成本为![]() 元件的工艺品投放市场进行试销,经过调查,得到如下数据:
元件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | ··· |
|
|
|
| ··· |
每天销售量 | ··· |
|
|
|
| ··· |
(1)若![]() 是
是![]() 的一次函数,求出此函数的关系式:
的一次函数,求出此函数的关系式:
(2)若用![]() (元)表示工艺厂试销该工艺品每天获得的利润,试求
(元)表示工艺厂试销该工艺品每天获得的利润,试求![]() (元)与
(元)与![]() (元/件)之间的函数关系式.
(元/件)之间的函数关系式.
(3)若该工艺品的每天的总成木不能超过![]() 元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?