题目内容
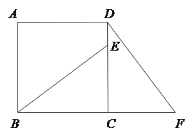
【题目】已知：如图，在正方形ABCD中，E是CD边上的一点，F为BC延长线上一点，且CE=CF．
（1）求证：△BEC≌△DFC；
（2）如果BC+DF=9，CF=3，求正方形ABCD的面积．
【答案】（1）证明见解析
（2）16
【解析】
试题（1）正方形的四个边相等，四个角都是直角，因此可得到BC=DC，∠ECD=∠FCD，由SAS可证明三角形全等．
（2）设BC=x，则CD=x，DF=9﹣x，CF=4，可用勾股定理求出x，因此可求出正方形ABCD的面积．
试题解析：（1）∵四边形ABCD是正方形
∴BC=CD，∠BCE=90°
∴∠DCF=180°-∠BCE=90°=∠BCE
在△BCE和△DCF中，
，
∴△BEC≌△DFC（SAS）；
（2）设BC=x，则CD=x，DF=9﹣x，
在Rt△DCF中，CF=3，
∴CF2+CD2=DF2，
32+x2=（9﹣x）2，
解得x=4，正方形的面积为：4×4=16．
练习册系列答案
名校课堂系列答案
相关题目
