Question

如图,将一个三角形的三边依次都分成2、3、4……等分,并将分点按图1、图2、图3那样连起来,这样,每个图中所得到的小三角形都会全等.按此方法,当三边都分成10等分时,所得到的全等小三角形的个数是(    ).

 

 

 

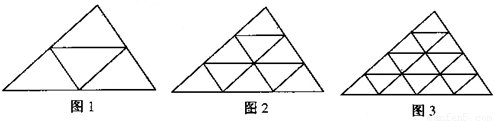
A . 98           B . 99             C . 100         D. 101

 

Answer 1

【答案】

C

【解析】本题考查的是图形的变化

第一图形中三角形的个数为4，第二个图形中三角形的个数为9，这两个数均为完全平方数，那么就可得到第n个图形中全等的三角形个数．

由图可知（1）中顺次连接各中点所得全等的小三角形为；

（2）中顺次连接各中点所得全等的小三角形为；

同理如果把三条边分成3等分可得到个全等的小三角形，

按照这种方式分下去，第n个图形中应该得到个全等的小三角形．

10等分时，n=9，

∴当三边都分成10等分时，所得到的全等小三角形的个数是．

故选C．