题目内容
 如图所示,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则EF的长是
如图所示,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则EF的长是3
3
.分析:根据正方形的性质得AB=BC,∠ABC=90°,再根据等角的余角相等得到∠EAB=∠FBC,则可根据“ASA”判断△ABE≌△BCF,所以BE=CF=2,进而求出EF的长.
解答:解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥BE,CF⊥BF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(ASA)
∴BE=CF=2,AE=BF=1,
∴EF=BE+BF=3,
故答案为3.
∴AB=BC,∠ABC=90°,
∵AE⊥BE,CF⊥BF,

∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
|
∴△ABE≌△BCF(ASA)
∴BE=CF=2,AE=BF=1,
∴EF=BE+BF=3,
故答案为3.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了正方形的性质以及勾股定理.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目



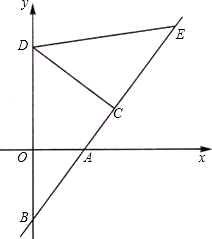 的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解.
的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解. :
: 与
与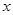 轴负半轴、
轴负半轴、 轴正半轴分别交于
轴正半轴分别交于 、
、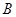 两点.
两点.
 时,试确定直线
时,试确定直线 为
为 延长线上一点,连接
延长线上一点,连接 ,过
,过 于
于 ,
, 于
于 ,若
,若 ,
, ,求
,求 的长;
的长; 取不同的值时,点
取不同的值时,点 、
、 和等腰直角
和等腰直角 ,连
,连 交
交 点,问当点
点,问当点 的长是否为定值,若是,请求出其值;若不是,请说明理由.
的长是否为定值,若是,请求出其值;若不是,请说明理由.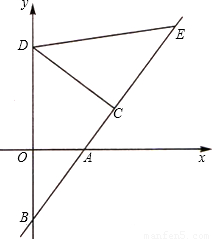
 :
: 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于
轴正半轴分别交于 、
、 两点.
两点.
 时,试确定直线
时,试确定直线 为
为 延长线上一点,连接
延长线上一点,连接 ,过
,过 于
于 ,
, 于
于 ,若
,若 ,
, ,求
,求 的长;
的长; 取不同的值时,点
取不同的值时,点 、
、 和等腰直角
和等腰直角 ,连
,连 交
交 点,问当点
点,问当点 的长是否为定值,若是,请求出其值;若不是,请说明理由.
的长是否为定值,若是,请求出其值;若不是,请说明理由.