题目内容
如图①所示,直线 :
: 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于
轴正半轴分别交于 、
、 两点.
两点.

(1)当 时,试确定直线
时,试确定直线 的解析式;
的解析式;
(2)在(1)的条件下,如图②所示,设 为
为 延长线上一点,连接
延长线上一点,连接 ,过
,过 、
、 两点分别作
两点分别作 于
于 ,
, 于
于 ,若
,若 ,
, ,求
,求 的长;
的长;
(3)当 取不同的值时,点
取不同的值时,点 在
在 轴正半轴上运动,分别以
轴正半轴上运动,分别以 、
、 为边在第一、第二象限作等腰直角
为边在第一、第二象限作等腰直角 和等腰直角
和等腰直角 ,连
,连 交
交 轴于
轴于 点,问当点
点,问当点 在
在 轴上运动时,试猜想
轴上运动时,试猜想 的长是否为定值,若是,请求出其值;若不是,请说明理由.
的长是否为定值,若是,请求出其值;若不是,请说明理由.
(1)直线l的解析式为y=x+5(2)AM=4(3)
【解析】
试题分析:解:(1)由题知,k≠0.把x=0代入y=kx+5k中,得y=5k;把y=0代入y=kx+5k中,得x=-5.∴A(-5,0),B(0,5k),∵点B在y轴正半轴上,∴5k>0.即OA=5,OB=5k.
∵OA=OB,∴k=1.∴直线l的解析式为y=x+5.
(2)法1:由(1)知,k=1,∴OA=5,OB=5.∵BN⊥OQ,AM⊥OQ,∴∠AMO=BNO=90°.
∵BN=3,∴在Rt△BON中, .
.
∵MN=7,∴OM=3.∴在Rt△AMO中, .
.
法2:由(1)知,OA=OB.∵AM⊥OQ,BN⊥OQ,∴∠AMO=BNO=90°,∴∠3+∠2=90°.
∵∠AOB=90°,∴∠1+∠2=90°,∴∠1=∠3,∴△AOM≌△OBN(AAS).
∴AM=ON,OM=BN=3.∵MN=7∴AM=ON=4
(3)PB长为定值.
法1:如图,过点E作EC⊥y轴于C,则∵△ABE为等腰直角三角形
∴AB=BE,∠ABE=90°.由(2)法2易证,△AOB≌△BCE(AAS),∴BC=OA=5,CE=OB.
∵△OBF为等腰直角三角形,∴OB=BF,∠OBF=90°.∴BF=CE,∠PBF=∠PCE=90°.
∵∠1=∠2,∴△PBF≌△PCE(AAS), ,即PB长为
,即PB长为 .
.
法二:由△AOB≌△BCE,可求E(-5k,5k+5).∵F(5k,5k),

考点:全等三角形及勾股定理等
点评:本题难度较大,主要考查学生对全等三角形及勾股定理等知识点综合分析能力,注意培养数形结合思想,灵活运用掌握的几何性质定理,运用到考试考题中去。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案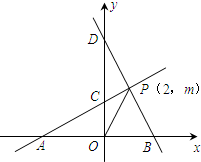 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.



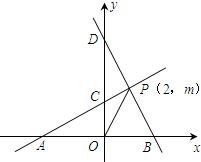 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.