题目内容
 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=| 1 |
| x |
分析:易得点B的坐标,设点E的纵坐标为y,可表示出点E的横纵坐标,代入所给反比例函数即可求得点E的纵坐标,也就求得了点E的横坐标.
解答:解:∵四边形OABC是正方形,点B在反比例函数y=
(k≠0)的图象上,
∴点B的坐标为(1,1).
设点E的纵坐标为y,
∴点E的横坐标为(1+y),
∴y×(1+y)=1,
即y2+y-1=0,
即y=
=
,
∵y>0,
∴y=
,
∴点E的横坐标为1+
=
.
故选:D.
| 1 |
| x |
∴点B的坐标为(1,1).
设点E的纵坐标为y,
∴点E的横坐标为(1+y),
∴y×(1+y)=1,
即y2+y-1=0,
即y=
-1±
| ||
| 2×1 |
-1±
| ||
| 2 |
∵y>0,
∴y=
| ||
| 2 |
∴点E的横坐标为1+
| ||
| 2 |
| ||
| 2 |
故选:D.
点评:此题主要考查了反比例函数的比例系数的意义;突破点是得到点B的坐标;用到的知识点为:在反比例函数图象上的点的横、纵坐标的积等于反比例函数的比例系数.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 如图,在正方形ABCD中,两条对角线AC,BD交于点O.
如图,在正方形ABCD中,两条对角线AC,BD交于点O.
 为线段
为线段 上任一点,写出变化后点
上任一点,写出变化后点 的对应点
的对应点 的坐标 ( ).
的坐标 ( ).
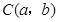 为线段
为线段 上任一点,写出变化后点
上任一点,写出变化后点 的对应点
的对应点 的坐标
( ).
的坐标
( ). 如图,在正方形ABCD中,两条对角线AC,BD交于点O.
如图,在正方形ABCD中,两条对角线AC,BD交于点O.