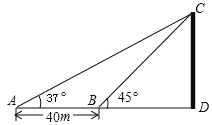
题目内容
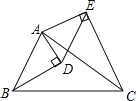
【题目】如图,等腰Rt△BPQ的顶点P在正方形ABCD的对角线AC上(P与AC不重合),∠PBQ=90°,QP与BC交于E,QP延长线交AD于F,连CQ.
(1)①求证:AP=CQ ;
②求证:![]()
(2)当![]() 时,求
时,求![]() 的值.
的值.
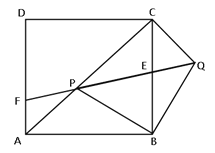
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】
(1)①证出∠ABP=∠CBQ,由SAS证明△ABP≌△CBQ可得结论;
②根据正方形的性质和全等三角形的性质得到∠DAC=∠BAC,∠APF=∠ABP,即可证得△APF∽△ABP,再根据相似三角形的性质即可求解;
(2)设正方形边长为![]() ,根据已知条件可求得PA的长,再根据第(1)②的结论可求得AF的长,从而求得答案.
,根据已知条件可求得PA的长,再根据第(1)②的结论可求得AF的长,从而求得答案.
证明:
(1)①∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△PBQ为等腰直角三角形,
∴∠PBQ=90°,PB=BQ,
∵∠ABP+∠BPC =∠BPC+∠CBQ=![]() ,
,
∴∠ABP=∠CBQ,
在△ABP与△CBQ中,
 ,
,
∴△ABP≌△CBQ,
∴AP=CQ;
②如图,

∵∠CPB=∠3+∠4=∠1+∠2,
∵∠4=∠1=45°,
∴∠3=∠2,
∴∠5=∠2,
∵∠6=∠1=45°,
∴△PFA∽△BPA,
∴![]() ,
,
∴![]() 即
即![]() ;
;
(2)设正方形边长为![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴PA=![]() ,
,
∵![]() ,
,
∴ ,
,
解得:AF=![]() ,
,
∴DF=![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目