解不等式组:$\left\{\begin{array}{l}{2x+3≥x+11}\\{\frac{2x+5}{3}-1＜2-x}\end{array}\right.$.并把解集在数轴上表示出来．题目和参考答案——青夏教育精英家教网—

题目内容

3．解不等式组：$\left\{\begin{array}{l}{2x+3≥x+11}\\{\frac{2x+5}{3}-1＜2-x}\end{array}\right.$，并把解集在数轴上表示出来．

分析分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．

解答解：解不等式2x+3≥x+11，得：x≥8，
解不等式$\frac{2x+5}{3}$-1＜2-x，得：x＜$\frac{4}{5}$，
表示在数轴上如下：

∴该不等式组无解．

点评本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．

练习册系列答案

相关题目

19．

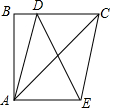如图，在Rt△ABC中，∠ABC=90°，AB=BC=2，点D在BC上，以AC为对角线的所有?ADCE中DE的最小值是（　　）

14．

小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带来了两块碎玻璃，其编号应该是②③．

11．要使分式$\frac{x-3}{2-x}$有意义，则x的取值应满足（　　）

18．在①-a⁵•（-a）²；②（-a⁶）÷（-a³）；③（-a²）³•（a³）²；④[-（-a）²]⁵中计算结果为-a¹⁰的有（　　）

15．解不等式组：$\left\{\begin{array}{l}{3x+7≥5（x-1）}\\{\frac{3x-2}{2}＞x+1}\end{array}\right.$，并在数轴上表示不等式组的解集．

12．我们把两条中线互相垂直的三角形称为“中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”，设BC=a，AC-b，AB=c．
【特例探索】
（1）如图1，当∠ABE=45°，c=2$\sqrt{2}$时，a=2$\sqrt{5}$，b=2$\sqrt{5}$；如图2，当∠ABE=30°，c=4时，a=2$\sqrt{13}$，b=2$\sqrt{7}$；
【归纳证明】
（2）请你观察（1）中的计算结果，猜想a²，b²，c²三者之间的关系，用等式表示出来，请利用图3证明你发现的关系式；
【拓展应用】
（3）如图4，在?ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD=2$\sqrt{5}$，AB=3．求AF的长．

13．33.33°=33^°19′48''；25°53'24''=25.89^°．

试题分类