��Ŀ����
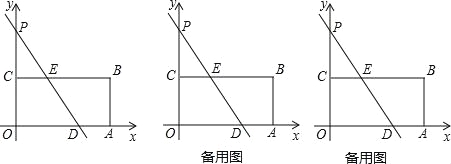
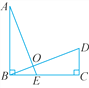
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A(a��1��a��b)��B(a��0)����(a��b��3)2��|a��2b|=0��CΪx���ϵ�B�Ҳ�Ķ��㣬��ACΪ��������������ACD��ʹAD=AC����CAD=��OAB��ֱ��DB��y���ڵ�P.
��1���߶�AO���߶�AB��������ϵ��______������>�������ݡ������ܡ�����<������=������
��2����֤����AOC�ա�ABD��
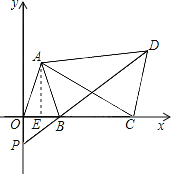
��3������CAD=30![]() ������C�˶�ʱ����P��y���ϵ�λ���Ƿ����ı䣬Ϊʲô��
������C�˶�ʱ����P��y���ϵ�λ���Ƿ����ı䣬Ϊʲô��
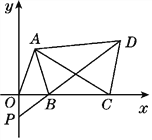
���𰸡���1����ȣ���2��֤������������3)λ�ò������ı�
����������������� ![]() �ȸ��ݷǸ������������
�ȸ��ݷǸ������������![]() ��ֵ����
��ֵ����![]() �ڵ�
�ڵ�![]() ����
����![]() �����ó�
�����ó�![]() ����ȫ�������ε����ʼ��ɵó�����.
����ȫ�������ε����ʼ��ɵó�����.![]() �ȸ���
�ȸ���![]() �ó�
�ó�![]() ����
����![]() �������ɵó�
�������ɵó�![]()
![]() ��
��![]() ��ȫ�������ε����ʿɵó�
��ȫ�������ε����ʿɵó�![]() ��
��![]() Ϊ��ֵ������
Ϊ��ֵ������![]() ��֪
��֪![]() �ij��Ȳ��䣬�ʿɵó����ۣ�
�ij��Ȳ��䣬�ʿɵó����ۣ�
���������
![]() ֤����
֤����![]()
![]() ���
���![]()
![]()
��![]() �ڵ�
�ڵ�![]() ��
��
![]()
![]()
��![]() ��
��![]() ��
�У�
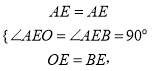
![]()
![]()
![]() ֤����
֤���� ![]()
![]()
��![]()
��![]() ��
��![]() ��
�У�
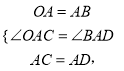
![]()
![]() ��
��![]() ��
��![]() ���ϵ�λ�ò������ı�.
���ϵ�λ�ò������ı�.
���ɣ���![]()
����![]() ֪
֪![]()
![]()
![]() Ϊ��ֵ,
Ϊ��ֵ,
![]()
��![]() ���Ȳ��䣬
���Ȳ��䣬
��![]() ��
��![]() ���ϵ�λ�ò������ı�.
���ϵ�λ�ò������ı�.

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ