题目内容
李明准备进行如下操作实验,把一根长40cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48cm2,你认为他的说法正确吗?请说明理由.
【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】(1)设剪成的较短的这段为xcm,较长的这段就为(40﹣x)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于58cm2建立方程求出其解即可;
(2)设剪成的较短的这段为mcm,较长的这段就为(40﹣m)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于48cm2建立方程,如果方程有解就说明李明的说法错误,否则正确.
【解答】解:(1)设剪成的较短的这段为xcm,较长的这段就为(40﹣x)cm,由题意,得
(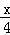 )2+(
)2+(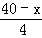 )2=58,
)2=58,
解得:x1=12,x2=28,
当x=12时,较长的为40﹣12=28cm,
当x=28时,较长的为40﹣28=12<28(舍去).
答:李明应该把铁丝剪成12cm和28cm的两段;
(2)李明的说法正确.理由如下:
设剪成的较短的这段为mcm,较长的这段就为(40﹣m)cm,由题意,得
(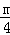 )2+(
)2+(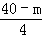 )2=48,
)2=48,
变形为:m2﹣40m+416=0,
∵△=(﹣40)2﹣4×416=﹣64<0,
∴原方程无实数根,
∴李明的说法正确,这两个正方形的面积之和不可能等于48cm2.
【点评】本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,根的判别式的运用,解答本题时找到等量关系建立方程和运用根的判别式是关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目


 F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:
F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据: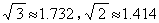 ,结果保留整数)
,结果保留整数)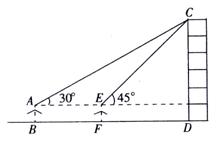
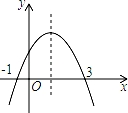
 .
.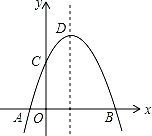
 的图象经过点P(-1,1),则k的值是
的图象经过点P(-1,1),则k的值是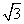 ≈1.732,100 km/h≈27.8m/s)
≈1.732,100 km/h≈27.8m/s)