Question

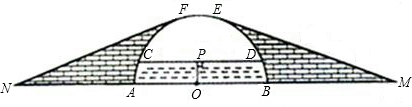
某河道上有一个半圆形的拱桥，河两岸筑有拦水堤坝，其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切，上、下桥斜面的坡度i＝1∶3.7，桥下水深OP＝5米，水面宽度CD＝24米.设半圆的圆心为O，直径AB在坡角顶点M、N的连线上，求从M点上坡、过桥、下坡到N点的最短路径长.（参考数据：π≈3，≈1.7，tan15°＝

Answer 1

解：连结OD、OE、OF，由垂径定理知：PD＝CD＝12（m）
    在Rt△OPD中，OD＝＝13（m）
    ∴OE＝OD＝13m
    ∵tan∠EMO=i= 1∶3.7 ，tan15°＝=≈1：3.7
    ∴∠EMO＝15°
    由切线性质知∠OEM＝90°∴∠EOM=75°
    同理得∠NOF＝75°∴∠EOF＝180°-75°×2＝30°
    在Rt△OEM中，tan15°＝=≈1∶3.7

        ∴EM＝3.7×13＝48.1（m）
又EF的弧长＝＝6.5（m）
∴48.1×2+6.5＝102.7（m）,
即从M点上坡、过桥、再下坡到N点的最短路径长为102.7米
（注：答案在102.5m—103m间只要过程正确，不扣分）