题目内容
在△ABC中,∠BAC:∠ABC:∠ACB=4:2:1,AD是∠BAC的平分线,有如下三个结论:①BC:AC:AB=4:2:1;②AC=AD+AB;③△DAC∽△ABC.其中正确的结论是
- A.①②
- B.②③
- C.①③
- D.①②③
B
分析:①中可根据正弦定理 进行验证,②中由全等可得线段相等,③中对应角相等,则两三角形相似.
进行验证,②中由全等可得线段相等,③中对应角相等,则两三角形相似.
解答: 解:如图所示①中,∠BAC:∠ABC:∠ACB=4:2:1,
解:如图所示①中,∠BAC:∠ABC:∠ACB=4:2:1,
但sin∠BAC:sin∠ABC:sin∠ACB≠4:2:1,
且 ,
,
所以①不正确;
②中由题中比例及AD平分∠BAC可知,∠BAD=∠B,
即AD=BD,
∵DF=DG,
∴DE=AD,△ABD≌△AED,
∴AE=AB
∴∠DEA=∠DAC,
∴EC=ED=AD,
∴AC=AE+EC=AB+AD,
所以②正确;
③中∠C为公共角,∠DAC=∠ABC,所以△DAC∽△ABC,故正确.
故选B.
点评:熟练掌握三角形的性质,角平分线的定义及三角形内角和定理.
分析:①中可根据正弦定理
 进行验证,②中由全等可得线段相等,③中对应角相等,则两三角形相似.
进行验证,②中由全等可得线段相等,③中对应角相等,则两三角形相似.解答:
 解:如图所示①中,∠BAC:∠ABC:∠ACB=4:2:1,
解:如图所示①中,∠BAC:∠ABC:∠ACB=4:2:1,但sin∠BAC:sin∠ABC:sin∠ACB≠4:2:1,
且
 ,
,所以①不正确;
②中由题中比例及AD平分∠BAC可知,∠BAD=∠B,
即AD=BD,
∵DF=DG,
∴DE=AD,△ABD≌△AED,
∴AE=AB
∴∠DEA=∠DAC,
∴EC=ED=AD,
∴AC=AE+EC=AB+AD,
所以②正确;
③中∠C为公共角,∠DAC=∠ABC,所以△DAC∽△ABC,故正确.
故选B.
点评:熟练掌握三角形的性质,角平分线的定义及三角形内角和定理.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.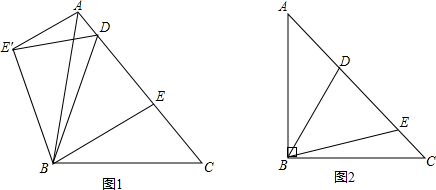
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.