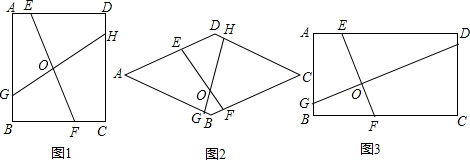
题目内容
如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,
上,
若![]() 90°,且
90°,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() 。
。
(1)图1中若点![]() 是边
是边![]() 的中点,我们可以构造两个三角形全等来证明
的中点,我们可以构造两个三角形全等来证明![]() ,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(3分)
,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(3分)
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合)。
重合)。
①![]() 是否总成立?请给出证明;(5分)
是否总成立?请给出证明;(5分)
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在抛物线
恰好落在抛物线![]() 上,求此时点
上,求此时点![]() 的坐标.(4分)
的坐标.(4分)
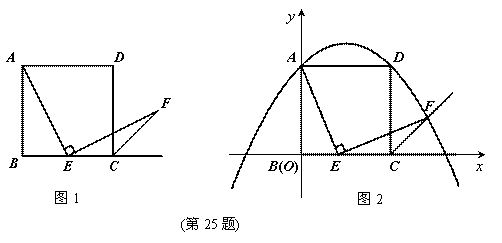

解:(1)如图1,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
△![]() 与△
与△![]() 全等.
全等.
(2)①若点![]() 在线段
在线段![]() 上滑动时
上滑动时![]() 总成立.
总成立.
证明:如图2,在![]() 上截取
上截取![]() . ∵
. ∵![]() ,∴
,∴![]() ,
,
∴△![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
又![]() 平分正方形的外角,∴
平分正方形的外角,∴![]() ,
,
∴![]() . 而
. 而![]() ,
,
∴![]() , ∴△
, ∴△![]() ≌△
≌△![]() .
.
∴![]() .
.

②过点![]() 作
作![]() 轴于
轴于![]() , 由①知,
, 由①知,![]() ,
,
设![]() ,则
,则![]() ,
,
∴点![]() 的坐标为
的坐标为![]() . ∵点
. ∵点![]() 恰好落在抛物线
恰好落在抛物线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,![]() (负值不合题意,舍去),
(负值不合题意,舍去),
∴![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目