题目内容
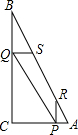 已知直角三角形ABC中,∠C=90°,AC=a,BC=2a.在AC、BC上分别有一动点P、Q,且PQ始终平分△ABC的面积.作PR⊥CA交AB于R,QS⊥BC交AB于S.线段BS、SR、RA能否构成一个直角三角形,证明你的猜想.
已知直角三角形ABC中,∠C=90°,AC=a,BC=2a.在AC、BC上分别有一动点P、Q,且PQ始终平分△ABC的面积.作PR⊥CA交AB于R,QS⊥BC交AB于S.线段BS、SR、RA能否构成一个直角三角形,证明你的猜想.
证明:∵直角三角形ABC中,∠C=90°,AC=a,BC=2a,
∴AB= =
= a,
a,
设CP=b,则AP=a-b,
设CQ=x,∵S△CPQ= S△ABC,即
S△ABC,即 bx=
bx= ×
× a•2a,
a•2a,
∴x= ,即CQ=
,即CQ= ,BQ=2a-
,BQ=2a- =
=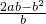 .
.
∵PR∥BC,
∴△APR∽△ACB,
∴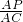 =
= ,
,
∴AR= =
=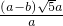 =
= (a-b),
(a-b),
同理,BS=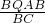 =
=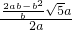 =
=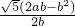 ,
,
∴SR= a-
a- (a-b)-
(a-b)-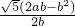 =
= =
=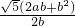 .
.
∵[ (a-b)]2+{
(a-b)]2+{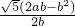 ]2=[
]2=[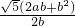 ]2,
]2,
即AR2+BS2=SR2.
∴线段BS、SR、RA能构成一个直角三角形.
分析:设CP=b,则可以用b表示出AP的长,然后利用S△CPQ= S△ABC,表示出BQ的长,根据△APR∽△ACB,相似三角形的对应边的比相等,即可利用a、b表示出AR的长,同理可以表示出BS的长,则ER可以表示出,然后利用勾股定理的逆定理即可判断.
S△ABC,表示出BQ的长,根据△APR∽△ACB,相似三角形的对应边的比相等,即可利用a、b表示出AR的长,同理可以表示出BS的长,则ER可以表示出,然后利用勾股定理的逆定理即可判断.
点评:本题考查了勾股定理的逆定理,以及相似三角形的性质,正确表示出AR的长度是关键.
∴AB=
 =
= a,
a,设CP=b,则AP=a-b,
设CQ=x,∵S△CPQ=
 S△ABC,即
S△ABC,即 bx=
bx= ×
× a•2a,
a•2a,
∴x=
 ,即CQ=
,即CQ= ,BQ=2a-
,BQ=2a- =
=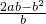 .
.∵PR∥BC,
∴△APR∽△ACB,
∴
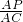 =
= ,
,∴AR=
 =
=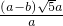 =
= (a-b),
(a-b),同理,BS=
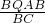 =
=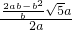 =
=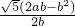 ,
,∴SR=
 a-
a- (a-b)-
(a-b)-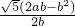 =
= =
=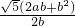 .
.∵[
 (a-b)]2+{
(a-b)]2+{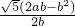 ]2=[
]2=[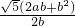 ]2,
]2,即AR2+BS2=SR2.
∴线段BS、SR、RA能构成一个直角三角形.
分析:设CP=b,则可以用b表示出AP的长,然后利用S△CPQ=
 S△ABC,表示出BQ的长,根据△APR∽△ACB,相似三角形的对应边的比相等,即可利用a、b表示出AR的长,同理可以表示出BS的长,则ER可以表示出,然后利用勾股定理的逆定理即可判断.
S△ABC,表示出BQ的长,根据△APR∽△ACB,相似三角形的对应边的比相等,即可利用a、b表示出AR的长,同理可以表示出BS的长,则ER可以表示出,然后利用勾股定理的逆定理即可判断.点评:本题考查了勾股定理的逆定理,以及相似三角形的性质,正确表示出AR的长度是关键.

练习册系列答案
相关题目
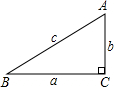 如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )
如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 21、根据下列语句作图、测量和比较.
21、根据下列语句作图、测量和比较. 已知直角三角形ABC中,∠C=90°,BC=6,CA=3,CD为∠C的角平分线,则CD=
已知直角三角形ABC中,∠C=90°,BC=6,CA=3,CD为∠C的角平分线,则CD=