题目内容
 在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:

请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin20°≈ ,cos20°≈
,cos20°≈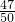 ,tan20°≈
,tan20°≈ )
)
解:由题意得∠ABC=90°
∵∠ACB=45°
∴∠CAB=90°-∠ACB=90°-45°=45°
∴AB=BC
设AB=x,则BC=x,DB=20+x
在Rt△ABD中
∵tan∠ADB=
∴tan20°= ,
,
∵tan20°= ,
,
∴ ,
,
x=11.25
∵BM=CE=1.5
∴AM=11.25+1.5=12.75
答:教学楼的高AM是12.75米.
方法二
解:设BD为x,则BC=x-20
∵∠ACB=45°,∠ABC=90°
∴∠CAB=45°
∴AB=BC=x-20
在Rt△ABD中
∵tan∠ADB=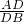 ,
,
∴tan20°= ,
,
∵tan20°= ,
,
∴ ,
,
x=31.25
∴BC=31.25-20=11.25
∵BM=CE=1.5
∴AM=11.25+1.5=12.75.
答:教学楼的高AM是12.75米.
分析:设AB=x,则BC=x,DB=20+x,在Rt△△ABD中利用20°的锐角三角函数值即可求出BC的长,又因为AM=AB+BM,问题得解.
点评:本题考查了解直角三角形的应用,构造仰角所在的直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.
∵∠ACB=45°
∴∠CAB=90°-∠ACB=90°-45°=45°
∴AB=BC
设AB=x,则BC=x,DB=20+x
在Rt△ABD中
∵tan∠ADB=

∴tan20°=
 ,
,∵tan20°=
 ,
,∴
 ,
,x=11.25
∵BM=CE=1.5
∴AM=11.25+1.5=12.75
答:教学楼的高AM是12.75米.
方法二
解:设BD为x,则BC=x-20
∵∠ACB=45°,∠ABC=90°
∴∠CAB=45°
∴AB=BC=x-20
在Rt△ABD中
∵tan∠ADB=
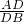 ,
,∴tan20°=
 ,
,∵tan20°=
 ,
,∴
 ,
,x=31.25
∴BC=31.25-20=11.25
∵BM=CE=1.5
∴AM=11.25+1.5=12.75.
答:教学楼的高AM是12.75米.
分析:设AB=x,则BC=x,DB=20+x,在Rt△△ABD中利用20°的锐角三角函数值即可求出BC的长,又因为AM=AB+BM,问题得解.
点评:本题考查了解直角三角形的应用,构造仰角所在的直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.

练习册系列答案
相关题目
 如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB. 根据他们测量的有关数据,解答下列问题:
根据他们测量的有关数据,解答下列问题: (2013•鄂尔多斯)在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
(2013•鄂尔多斯)在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
 如图,是一块四边形花园ABDC,在一次数学课外实践活动中,小刚量得∠A=90°,AC=3m,AB=4m,CD=
如图,是一块四边形花园ABDC,在一次数学课外实践活动中,小刚量得∠A=90°,AC=3m,AB=4m,CD=