题目内容
（2013•淄博）如图，AB是⊙O的直径， |
| AD |
|
| DE |
| 4 |
| 5 |
| 4 |
| 5 |
分析：连接AD，在Rt△ABD中利用勾股定理求出AD，证明△DAC∽△DBA，利用对应边成比例的知识，可求出CD、AC，继而根据sin∠ECB=sin∠DCA=
即可得出答案．
| AD |
| AC |
解答：
解：连接AD，则∠ADB=90°，
在Rt△ABD中，AB=5，BD=4，
则AD=
=3，
∵
=
，
∴∠DAC=∠DBA，
∴△DAC∽△DBA，
∴
=
=
，
∴CD=
，
∴AC=
=
，
∴sin∠ECB=sin∠DCA=
=
．
故答案为：
．
解：连接AD，则∠ADB=90°，在Rt△ABD中，AB=5，BD=4，
则AD=
| AB2-BD2 |
∵
|
| AD |
|
| DE |
∴∠DAC=∠DBA，
∴△DAC∽△DBA，
∴
| CD |
| AD |
| AD |
| BD |
| 3 |
| 4 |
∴CD=
| 9 |
| 4 |
∴AC=
| AD2+CD2 |
| 15 |
| 4 |
∴sin∠ECB=sin∠DCA=
| AD |
| AC |
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题考查了相似三角形的判定与性质，解答本题的关键是作出辅助线，证明△DAC∽△DBA，求出CD、AD的长度，难度一般．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
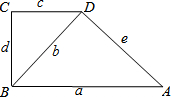（2013•淄博）如图，直角梯形ABCD中，AB∥CD，∠C=90°，∠BDA=90°，AB=a，BD=b，CD=c，BC=d，AD=e，则下列等式成立的是（ ）
（2013•淄博）如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）
（2013•淄博）如图，Rt△OAB的顶点A（-2，4）在抛物线y=ax2上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为（ ）
（2013•淄博）如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ的长为（ ）