Question

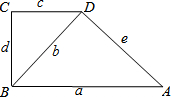（2013•淄博）如图，直角梯形ABCD中，AB∥CD，∠C=90°，∠BDA=90°，AB=a，BD=b，CD=c，BC=d，AD=e，则下列等式成立的是（　　）

A．b²=ac

B．b²=ce

C．be=ac

D．bd=ae

Answer 1

分析：根据∠CDB=∠DBA，∠C=∠BDA=90°，可判定△CDB∽△DBA，利用对应边成比例，即可判断各选项．

解答：解：∵CD∥AB，
∴∠CDB=∠DBA，
又∵∠C=∠BDA=90°，
∴△CDB∽△DBA，
∴

CD

DB

=

BC

AD

=

BD

AB

，即

c

b

=

d

e

=

b

a

，
A、b²=ac，成立，故本选项正确；
B、b²=ac，不是b²=ce，故本选项错误；
C、be=ad，不是be=ac，故本选项错误；
D、bd=ac，不是bd=ae，故本选项错误．
故选A．

点评：本题考查了相似三角形的判定与性质，解答本题的关键是判断△CDB∽△DBA，注意掌握相似三角形的对应边成比例．