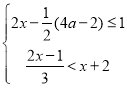题目内容
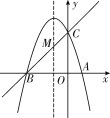
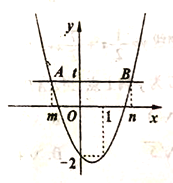
【题目】如图为二次函数![]() 图象,直线
图象,直线![]() 与抛物线交于
与抛物线交于![]() 两点,
两点,![]() 两点横坐标分别为
两点横坐标分别为![]() 根据函数图象信息有下列结论:
根据函数图象信息有下列结论:
①![]() ;
;
②若对于![]() 的任意值都有
的任意值都有![]() ,则
,则![]() ;
;
③![]() ;
;
④![]() ;
;
⑤当![]() 为定值时若
为定值时若![]() 变大,则线段
变大,则线段![]() 变长
变长
其中,正确的结论有__________(写出所有正确结论的番号)
【答案】①②③
【解析】
分别参考图像去解答,因为对称轴为正数,所以![]() 异号,根据与y轴交点为c得出
异号,根据与y轴交点为c得出![]() ,去判断各种情况,而且
,去判断各种情况,而且![]() 越大开口越小,进而得出正确答案即可.
越大开口越小,进而得出正确答案即可.
解:①中,![]() 对称轴为正数,所以
对称轴为正数,所以![]() 异号,
异号,
![]() 与y轴交点为
与y轴交点为![]() ,
,
![]() ,
,
![]() ,故①对;
,故①对;
②中,由图像得:![]() ,知道
,知道![]() ,
,
当函数与x轴左交点为![]() 时,代入函数表达式
时,代入函数表达式![]() 得:
得:
![]() ,
,
![]() ,此时考虑的是临界情况,
,此时考虑的是临界情况,
![]() 对于
对于![]() 的任意值都有
的任意值都有![]() ,则
,则![]() ,故②对;
,故②对;
③中,![]() 所对的值是关于对称轴对称的,
所对的值是关于对称轴对称的,
![]() 对称轴
对称轴![]() ,
,
![]() ,故③对;
,故③对;
④中无法确定;
⑤中,当![]() 为定值时若
为定值时若![]() 变大,则抛物线的开口变小,则线段
变大,则抛物线的开口变小,则线段![]() 变短,故⑤错;
变短,故⑤错;
故答案填:①②③.

【题目】空间任意选定一点![]() ,以点
,以点![]() 为端点,作三条互相垂直的射线
为端点,作三条互相垂直的射线![]() ,
,![]() ,
,![]() .这三条互相垂直的射线分别称作
.这三条互相垂直的射线分别称作![]() 轴、
轴、![]() 轴、
轴、![]() 轴,统称为坐标轴,它们的方向分别为
轴,统称为坐标轴,它们的方向分别为![]() (水平向前),
(水平向前),![]() (水平向右),
(水平向右),![]() (竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为
(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为![]() ,
,![]() ,
,![]() ,且
,且![]() 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体
的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
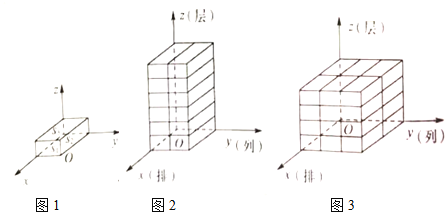
所在的面与![]() 轴垂直,如图1所示.若将
轴垂直,如图1所示.若将![]() 轴方向表示的量称为几何体码放的排数,
轴方向表示的量称为几何体码放的排数,![]() 轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了
轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() ,如图3的几何体码放了
,如图3的几何体码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() .这样我们就可用每一个有序数组
.这样我们就可用每一个有序数组![]() 表示一种几何体的码放方式.
表示一种几何体的码放方式.
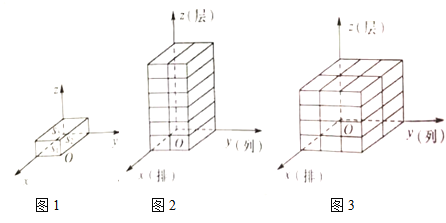
(1)有序数组![]() 所对应的码放的几何体是______________;
所对应的码放的几何体是______________;
A.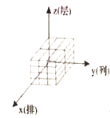 B.
B.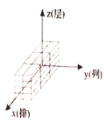 C.
C.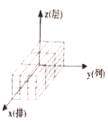 D.
D.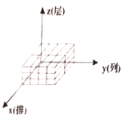
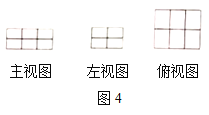
(2)图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(______,_______,_______),组成这个几何体的单位长方体的个数为____________个.
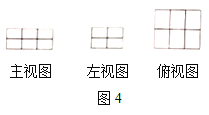
(3)为了进一步探究有序数组![]() 的几何体的表面积公式
的几何体的表面积公式![]() ,某同学针对若干个单位长方体进行码放,制作了下列表格:
,某同学针对若干个单位长方体进行码放,制作了下列表格:
几何体有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上规律,请直接写出有序数组![]() 的几何体表面积
的几何体表面积![]() 的计算公式;(用
的计算公式;(用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
(4)当![]() ,
,![]() ,
,![]() 时,对由
时,对由![]() 个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对
个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对![]() 个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
【题目】空间任意选定一点![]() ,以点
,以点![]() 为端点,作三条互相垂直的射线
为端点,作三条互相垂直的射线![]() ,
,![]() ,
,![]() .这三条互相垂直的射线分别称作
.这三条互相垂直的射线分别称作![]() 轴、
轴、![]() 轴、
轴、![]() 轴,统称为坐标轴,它们的方向分别为
轴,统称为坐标轴,它们的方向分别为![]() (水平向前),
(水平向前),![]() (水平向右),
(水平向右),![]() (竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为
(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为![]() ,
,![]() ,
,![]() ,且
,且![]() 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体
的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,如图1所示.若将
轴垂直,如图1所示.若将![]() 轴方向表示的量称为几何体码放的排数,
轴方向表示的量称为几何体码放的排数,![]() 轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了
轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() ,如图3的几何体码放了
,如图3的几何体码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() .这样我们就可用每一个有序数组
.这样我们就可用每一个有序数组![]() 表示一种几何体的码放方式.
表示一种几何体的码放方式.
(1)有序数组![]() 所对应的码放的几何体是______________;
所对应的码放的几何体是______________;
A.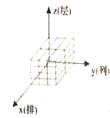 B.
B.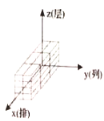 C.
C.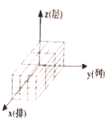 D.
D.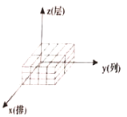
(2)图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(______,_______,_______),组成这个几何体的单位长方体的个数为____________个.
(3)为了进一步探究有序数组![]() 的几何体的表面积公式
的几何体的表面积公式![]() ,某同学针对若干个单位长方体进行码放,制作了下列表格:
,某同学针对若干个单位长方体进行码放,制作了下列表格:
几何体有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上规律,请直接写出有序数组![]() 的几何体表面积
的几何体表面积![]() 的计算公式;(用
的计算公式;(用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
(4)当![]() ,
,![]() ,
,![]() 时,对由
时,对由![]() 个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对
个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对![]() 个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)