题目内容
 如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,则∠DAE的度数为
如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,则∠DAE的度数为考点:翻折变换(折叠问题)
专题:
分析:如图,由三角形内角和定理求出∠B+∠C=40°;证明∠ADE+∠AED=2(α+β)=80°,即可解决问题.
解答: 解:如图,∵∠BAC=140°,
解:如图,∵∠BAC=140°,
∴∠B+∠C=180°-140°=40°;
由题意得:∠B=∠DAB(设为α),∠C=∠EAC(设为β),
∴∠ADE=2α,∠AED=2β,
∴∠DAE=180°-2(α+β)=180°-80°=100°,
故答案为100°.
 解:如图,∵∠BAC=140°,
解:如图,∵∠BAC=140°,∴∠B+∠C=180°-140°=40°;
由题意得:∠B=∠DAB(设为α),∠C=∠EAC(设为β),
∴∠ADE=2α,∠AED=2β,
∴∠DAE=180°-2(α+β)=180°-80°=100°,
故答案为100°.
点评:该题主要考查了旋转变换的性质、三角形的内角和定理及其应用问题;解题的关键是灵活运用旋转变换的性质、三角形的内角和定理来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中有一个点A(-
,1),在坐标轴上找一个点P,使得以A、P、O为顶点的三角形是等腰三角形,则这样的点P有( )
| 3 |
| A、5个 | B、6个 | C、7个 | D、8个 |
 如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从点C开始沿CB向点B以1cm/s的速度移动,点Q从A开始沿AC向点C以2cm/s的速度移动,如果点P,Q同时从点C,A出发,试问:
如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从点C开始沿CB向点B以1cm/s的速度移动,点Q从A开始沿AC向点C以2cm/s的速度移动,如果点P,Q同时从点C,A出发,试问: 如图,数轴上表示1、
如图,数轴上表示1、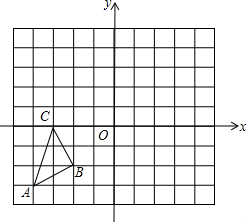 如图,在边长为1个单位长度的小正方形组成的网格中,O为坐标原点,A(-4,-3),B(-2,-2),C(-3,0).
如图,在边长为1个单位长度的小正方形组成的网格中,O为坐标原点,A(-4,-3),B(-2,-2),C(-3,0). (1)与∠E成内错角的是
(1)与∠E成内错角的是